Unbounded Knapsack Pattern
Introduction :
Given the weights and profits of ‘N’ items, put it in a knapsack of capacity ‘C’ such that we get the max profit.
Only difference between 0/1Knapsack and Unbounded knapsack is that here we are allowed to use an unlimited quantity of an item.
Example:
items: {Apple, Orange, Melon}
weights: {1, 2, 3}
profits: {15, 20, 50}
capacity: 5
Different Profit Combinations:
5 Apples (total weight 5) => 75 profit
1 Apple + 2 Oranges (total weight 5) => 55 profit
3 Apples + 1 Orange (total weight 5) => 65 profit
2 Apples + 1 Melon (total weight 5) => 80 profit
1 Orange + 1 Melon (total weight 5) => 70 profit
Best Profit Combination : 2 Apples + 1 Melon with 80 profit.
Problems following Unbounded Knapsack Pattern
1. Unbounded Knapsack
Problem:
Given the weights w and profits p of ‘N’ items, need to find a subset of these items which will give max profit with contstraint that their cumulative sum should not be greater than total knapsack capacity C.
Each item can only be selected multiple times.
Brute-Force : Recursive Solution
- Try all possible combination of given items and choose the one with maximum profits.
- The only difference from 0/1 knapsack is after including the item we recursively call to process all items (instead of remaining).
Code:
def unbounded_knapsack_recursion(weights, profits, capacity):
item_index = 0
return unbounded_knapsack_recursion_util(weights, profits, capacity, item_index)
def unbounded_knapsack_recursion_util(weights, profits, capacity, item_index):
if (capacity <= 0 or item_index >= len(profits)):
return 0
current_included_profit, current_excluded_profit = 0, 0
if(weights[item_index] <= capacity):
current_included_profit = profits[item_index] + \
unbounded_knapsack_recursion_util(weights, profits, capacity - weights[item_index], item_index)
current_excluded_profit = unbounded_knapsack_recursion_util(weights, profits, capacity, item_index + 1)
return max(current_included_profit, current_excluded_profit)
print("Recursive Method :")
print(unbounded_knapsack_recursion([1, 3, 4, 5], [15, 50, 60, 90], 8))
print(unbounded_knapsack_recursion([1, 3, 4, 5], [15, 50, 60, 90], 6))
Output:
140
105
Complexity:
- Time: O(2N+C) - Exponential with N+C, with N as no. of elements and C as knapsack capacity.
- Space: O(N+C) - To store the recursion stack. Max depth of recurstion stack is N+C.
DP : Recursion + Memoization (Top-Down) Solution
- We can use memoization to solve it in top-down manner.
Code:
def unbounded_knapsack_dp_memoization(weights, profits, capacity):
memory = [[None] * (capacity + 1) for i in range(len(weights))]
item_index = 0
return unbounded_knapsack_dp_memoization_util(weights, profits, capacity, item_index, memory)
def unbounded_knapsack_dp_memoization_util(weights, profits, capacity, item_index, memory):
if (capacity <= 0 or item_index >= len(profits)):
return 0
if (memory[item_index][capacity]):
return memory[item_index][capacity]
current_included_profit, current_excluded_profit = 0, 0
if(weights[item_index] <= capacity):
current_included_profit = profits[item_index] + \
unbounded_knapsack_dp_memoization_util(weights, profits, capacity - weights[item_index], item_index, memory)
current_excluded_profit = unbounded_knapsack_dp_memoization_util(weights, profits, capacity, item_index + 1, memory)
memory[item_index][capacity] = max(current_included_profit, current_excluded_profit)
return memory[item_index][capacity]
print("\nDP -> Recursion + Memoization Method :")
print(unbounded_knapsack_dp_memoization([1, 3, 4, 5], [15, 50, 60, 90], 8))
print(unbounded_knapsack_dp_memoization([1, 3, 4, 5], [15, 50, 60, 90], 6))
Output:
140
105
Complexity:
- Time: O(N*C) - Our memory stores the results for all the possible subproblems, hence we can’t have more than N*C subproblems.
- Space: O(N*C) - N*C space is used to store results and N for the recursion call stack and hence asymptotically O(N*C).
DP : Iteration + Tabulation (Bottom-Up) Solution
- Now we will try to solve the problem in bottom up fashion.
- We want to find the maximum profit for every sub-array and for every possible capacity.
- For every possbile capacity ‘c’ (0<=c<=capacity), we have two options.
- Exclude the item, in this case we will take whatever profit we get from the sub-array excluding this item table[index-1][c].
- Include the item if weight is lesser than capacity avaialble, in this we get profit by this item plus profit from remaining capacity profits[item_index] + table[index][c].
- Finally take the maximum of both.
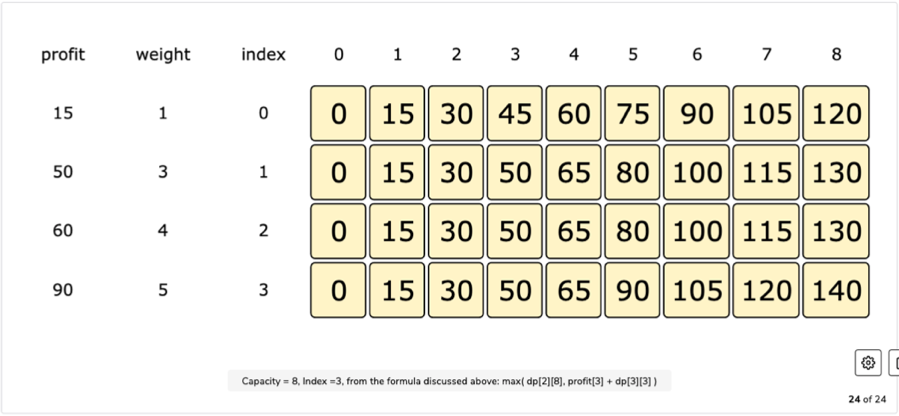
Table Filling Formula:
table[index][c] = max(table[index-1][c], profits[item_index] + table[index][c-weights[item_index]])
Tabulation:
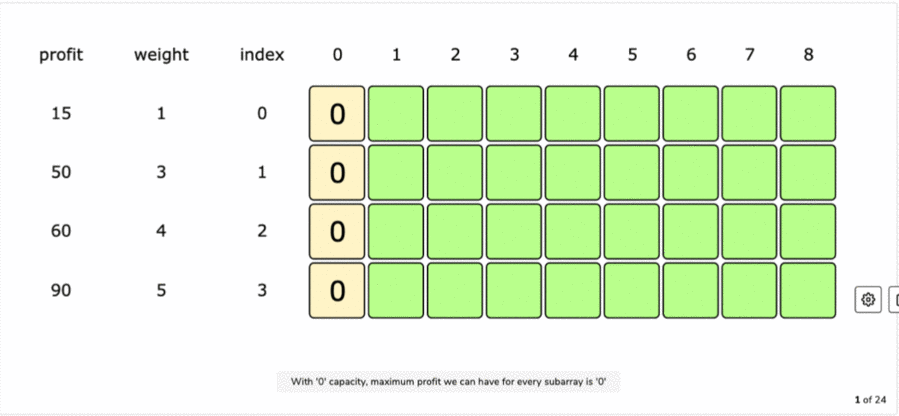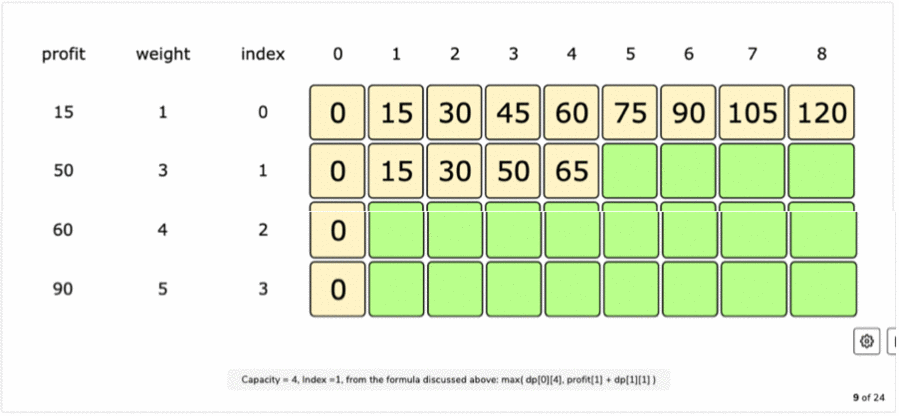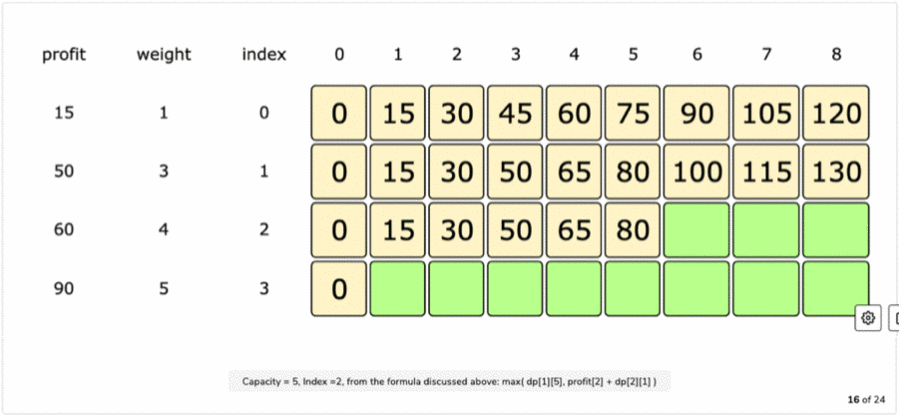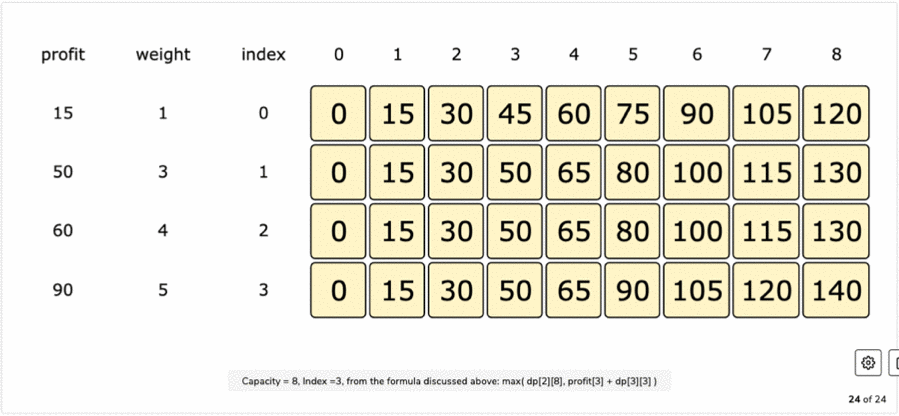
Final Table:
Code:
def unbounded_knapsack_dp_tabulation(weights, profits, capacity):
n = len(profits)
table = [[0] * (capacity + 1) for i in range(n)]
# When capacity is 0, none of the item can be selected
for i in range(n):
table[i][0] = 0
# When only 1 item is considered, get the profits using that item for every capapcity 'c'
for c in range(capacity + 1):
table[0][c] = (c // weights[0]) * profits[0]
# For each item, check for every possible capacities
for i in range(1, n):
for c in range(1, capacity + 1):
if (weights[i] <= c):
table[i][c] = max(table[i - 1][c], profits[i] + table[i][c - weights[i]])
else:
table[i][c] = table[i - 1][c]
return table[i][c]
print("\nDP -> Iteration + Tabulation Method :")
print(unbounded_knapsack_dp_tabulation([1, 3, 4, 5], [15, 50, 60, 90], 8))
print(unbounded_knapsack_dp_tabulation([1, 3, 4, 5], [15, 50, 60, 90], 6))
Output:
DP -> Iteration + Tabulation Method :
140
105
Complexity:
- Time: O(N*C)
- Space: O(N*C)
Finding Selected Items:
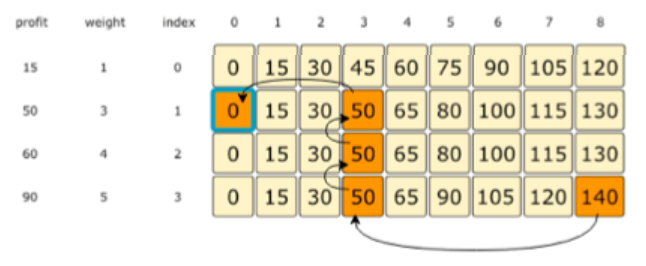
- Start from bottom right corener, in this case we have 140.
- Then check top cell (130 in this case), it is not coming from top cell, so we select this item (4th item) and subtract it profit and go to 50.
- Then we check that it comes from top cell (50), so we ignore it (4th item this time) and go to previous row.
- Now again this 50 comes from top, so we go to previous row and ignore (3rd item).
- Now this 50 doesn’t come from top which is 45, so we select this item (2nd item) and subtract its profit to go to 0.
- As we reach 0 now, so we are done picking the items.
Code:
def unbounded_knapsack_dp_tabulation(weights, profits, capacity):
n = len(profits)
table = [[0] * (capacity + 1) for i in range(n)]
# When capacity is 0, none of the item can be selected
for i in range(n):
table[i][0] = 0
# When only 1 item is considered, get the profits using that item for every capapcity 'c'
for c in range(capacity + 1):
table[0][c] = (c // weights[0]) * profits[0]
# For each item, check for every possible capacities
for i in range(1, n):
for c in range(1, capacity + 1):
if (weights[i] <= c):
table[i][c] = max(table[i - 1][c], profits[i] + table[i][c - weights[i]])
else:
table[i][c] = table[i - 1][c]
pick_selected_items(table, weights, profits)
return table[i][c]
def pick_selected_items(table, weights, profits):
i, c = len(table)-1, len(table[0])-1
total_profit = table[i][c]
print("Selected items are : ")
while (i-1 >= 0 and table[i][c] >= 0):
if (table[i][c] != table[i - 1][c]):
print(f"item - {i+1} with weight : {weights[i]} and profit : {profits[i]}")
c -= weights[i]
total_profit -= profits[i]
else:
i -= 1
while (total_profit > 0):
print(f"item - {1} with weight : {weights[0]} and profit : {profits[0]}")
total_profit -= profits[0]
print("\nDP -> Iteration + Tabulation Method :")
print(unbounded_knapsack_dp_tabulation([1, 3, 4, 5], [15, 50, 60, 90], 8))
print(unbounded_knapsack_dp_tabulation([1, 3, 4, 5], [15, 50, 60, 90], 6))
Output:
Selected items are :
item - 4 with weight : 5 and profit : 90
item - 2 with weight : 3 and profit : 50
140
Selected items are :
item - 4 with weight : 5 and profit : 90
item - 1 with weight : 1 and profit : 15
105
2. Rod Cutting
3. Coin Change
4. Minimum Coin Change
5. Maximum Ribbon Cut
← Previous: 0/1 Knapsack Pattern
Next: Palindromic Subsequence Pattern →