Home techblogs dynamic-programming-patterns 0-1-knapsack-pattern

0/1 Knapsack Pattern

Problems following 0/1 Knapsack Pattern

1. 0/1 Knapsack

Problem:

Given the weights w and profits p of ‘N’ items, need to find a subset of these items which will give max profit with contstraint that their cumulative sum should not be greater than total knapsack capacity C.

Each item can only be selected only once and each item will be either taken (1) or skipped (0).

Example:
Items: {Apple, Orange, Banana, Melon}
Weights(w): {2, 3, 1, 4}
Profits(p): {4, 5, 3, 7}
Knapsack Capacity(C): 5

Answer: 10 - Banana + Melon with total weight 5
All other combinations with weight 5 or less has lesser profits.

Brute-Force : Recursive Solution

• Try out all possible combinations of items which has cumulative weight less than given capacity and then pick one with highest profit.
• For every item take 2 possiblities first with including this item (if weight constraint is fine) and second with excluding this item.
• Finally we can get the set with max profit following the capacity constriant.

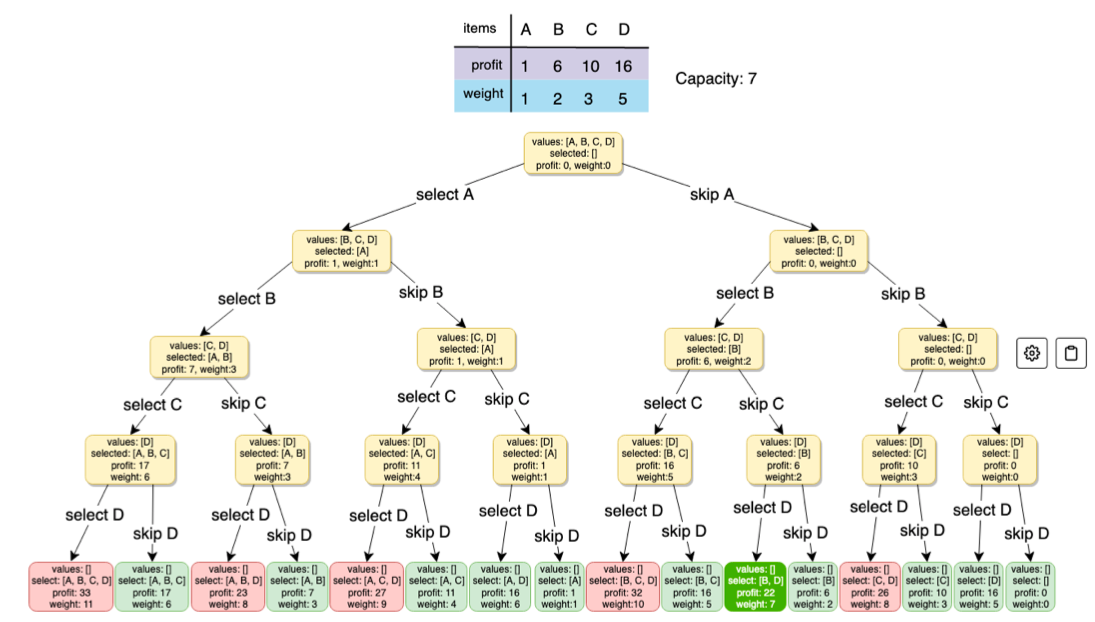
Code :

def solve_knapsack_recursion(profits, weights, capacity):
    item_index = 0
    return solve_knapsack_recursion_util(profits, weights, capacity, item_index)

def solve_knapsack_recursion_util(profits, weights, capacity, item_index):
    if (capacity <= 0 or item_index >= len(profits)):
        return 0

    profit1 = 0
    if (weights[item_index] <= capacity):  # can be included
        profit1 = profits[item_index] + solve_knapsack_recursion_util(profits, weights, 
        capacity-weights[item_index], item_index+1)
    
    profit2 = solve_knapsack_recursion_util(profits, weights, capacity, item_index+1)

    return max(profit1, profit2)


print("Recursive Method :")
print(solve_knapsack_recursion([1, 6, 10, 16], [1, 2, 3, 5], 7))
print(solve_knapsack_recursion([1, 6, 10, 16], [1, 2, 3, 5], 6))

Output:

Recursive Method :
22
17

Complexity:

• Time: O(2ⁿ) - Total no. of nodes we need to process is 2ⁿ + 2ⁿ-1.
• Space: O(n) - As we are going in depth first way at max n elements can be there in recursion stack

Identifying the problem as DP:

• Need to draw the recursive calls to see if there are any overlapping subproblems.
• In each recursive call, profits and weights array remain constant and only capacity and item index changes.
• Drawing recursive calls with denoting index as i and capacity as c.

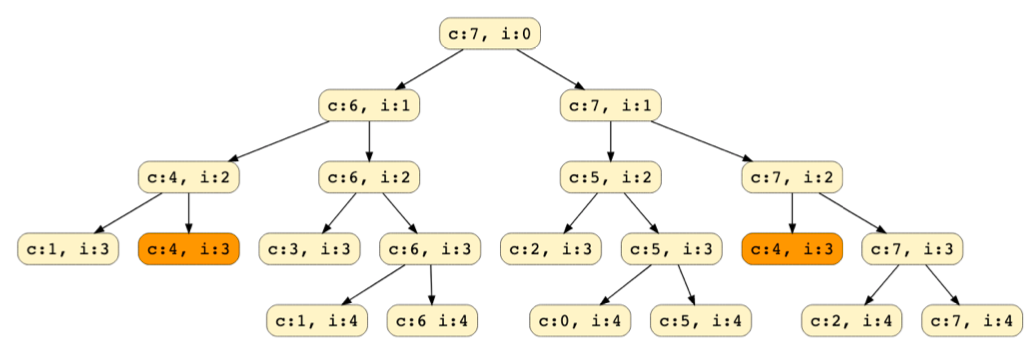
• Here we see that overlapping sublproblems as c:4, i:3 is repeating and hence can be solved using memoization.

DP : Recursion + Memoization (Top-Down) Solution

• As we can see that this has overlapping subproblems so we can use Memoization to solve this.

Code:

def solve_knapsack_dp_memoization(profits, weights, capacity):
    memory = [[None]*(capacity+1) for i in range(len(profits))]
    item_index = 0
    return solve_knapsack_dp_memoization_util(profits, weights, capacity, item_index, memory)

def solve_knapsack_dp_memoization_util(profits, weights, capacity, item_index, memory):
    if (capacity <= 0 or item_index >= len(profits)):
        return 0
    
    if(memory[item_index][capacity]):
        return memory[item_index][capacity]
    
    profit1 = 0
    if (weights[item_index] <= capacity):  # can be included
        profit1 = profits[item_index] + solve_knapsack_dp_memoization_util(profits, weights, 
        capacity-weights[item_index], item_index+1, memory)

    profit2 = solve_knapsack_dp_memoization_util(profits, weights, capacity, item_index+1, memory)
    memory[item_index][capacity] = max(profit1, profit2)

    return memory[item_index][capacity]


print("\nDP -> Recursion + Memoization Method :")
print(solve_knapsack_dp_memoization([1, 6, 10, 16], [1, 2, 3, 5], 7))
print(solve_knapsack_dp_memoization([1, 6, 10, 16], [1, 2, 3, 5], 6))

Output:

DP -> Recursion + Memoization Method :
22
17

Complexity:

• Time: O(N*C)
  • As we have memoized results of all the subproblems, we can conclude that we will not have more than N*C subproblems.
• Space: O(N*C)
  • In the worst case we will have to store NC** subproblems and also **O(N)** for recursion call stack. Overall it’s **O(NC).

DP : Iteration + Tabulation (Bottom-Up) Solution

• Now we willl try to build table in bottom up fashion.
• Here we need to find the max profit for every subarray for every possible capacity.
• table[i][c] will represent the max profit for capacity c from firs i items.
• For each item at index i (0<=i<items.length) and capacity c (0 <= c <= capacity) we have two options:
  1. Exclude the item at index i, in this case the we will get the profit we get from table[i-1][c].
  2. Inlude the item at index i, if its weight is not more than capacity, in this case we get profit that is profits[i] + table[i-1][c-weights[i]].
• Finally just get the max value from both the possbilities.

Table Filling Formula:

table[i][c] = max(table[i-1][c], profits[i] + table[i-1][c-weights[i])

Tabulation:

Final Table:

Code:

def solve_knapsack_dp_tabulation(profits, weights, capacity):
    table = [[0]*(capacity+1) for i in range(len(profits))]

    # When capacity is zero then, none of the item can be selected
    for i in range(len(profits)):
        table[i][0] = 0
    
    # If we consider only first weight, we will take it if its weight is less than capacity
    for c in range(capacity+1):
        if(weights[0] <= c):
            table[0][c] = profits[0]
    
    # Now consider rest by taking max of 1) current item can be included 2) current item is excluded
    for i in range(1, len(profits)):
        for c in range(1, capacity+1):
            if(weights[i] <= c):
                table[i][c] = max(table[i-1][c], profits[i] + table[i-1][c-weights[i]])
            else:
                table[i][c] = table[i-1][c]
    
    return table[i][c]


print("\nDP -> Iteration + Tabulation Method :")
print(solve_knapsack_dp_tabulation([1, 6, 10, 16], [1, 2, 3, 5], 7))
print(solve_knapsack_dp_tabulation([1, 6, 10, 16], [1, 2, 3, 5], 6))

Output:

DP -> Iteration + Tabulation Method :
22
17

Complexity:

• Time: O(N*C)
• Space: O(N*C)

Finding Selected Items:

• Profit 22 did not come from top cell (which is 17), hence we must include this item (item D with profit 16 and weight 5).
• Now if 22 did not come from top cell it should have come from table[i-1][c-weights[i] which is table[2][2] with profit 6.
• Now this 6 is coming from top cell so we will not include this item, so we move to table[1][2].
• Now this 6 is not coming from top cell so, we must include this item (item B with profit 6 and weight 2).
• Now it 6 did not come from top it would have come from table[i-1][c-weights[i] which is table[0][0] with profit 0.
• Once we hit zero profit we stop our picking.

Code:

def solve_knapsack_dp_tabulation(profits, weights, capacity):
    table = [[-1]*(capacity+1) for _ in range(len(profits))]

    # When capacity is zero then, none of the item can be selected
    for i in range(len(profits)):
        table[i][0] = 0

    # If we consider only first weight, we will take it if its weight is less than capacity
    for c in range(capacity+1):
        if(weights[0] <= c):
            table[0][c] = profits[0]

    # Now consider rest by taking max of 1) current item can be included 2) current item is excluded
    for i in range(1, len(profits)):
        for c in range(1, capacity+1):
            if(weights[i] <= c):
                table[i][c] = max(table[i-1][c], profits[i] + table[i-1][c-weights[i]])
            else:
                table[i][c] = table[i-1][c]

    pick_selected_items(table, weights, profits)

    return table[i][c]


def pick_selected_items(table, weights, profits):
    i, c = len(table) - 1, len(table[0]) - 1
    total_profit = table[i][c]

    print("Selected items are : ")

    while(total_profit > 0 and i-1 >= 0):
        if(table[i][c] != table[i-1][c]):
            print(f"item - {i+1} with weight : {weights[i]} and total_profit : {profits[i]}")
            total_profit -= profits[i]
            c -= weights[i]
        i -= 1

    if total_profit != 0:
        print(f"item - {1} with weight : {weights[0]} and total_profit : {profits[0]}")


print("\nDP -> Iteration + Tabulation Method :")
print(solve_knapsack_dp_tabulation([1, 6, 10, 16], [1, 2, 3, 5], 7))
print(solve_knapsack_dp_tabulation([1, 6, 10, 16], [1, 2, 3, 5], 6))

Output:

DP -> Iteration + Tabulation Method :
Selected items are : 
item - 4 with weight : 5 and total_profit : 16
item - 2 with weight : 2 and total_profit : 6
22
Selected items are : 
item - 3 with weight : 3 and total_profit : 10
item - 2 with weight : 2 and total_profit : 6
item - 1 with weight : 1 and total_profit : 1
17

Space Optimized Solution : Solving in O(C) space

• If we see closely, we need two values from the previous iteration table[c] and table[c-weights[i]].
• Since our inner loop is iterating over c: 0–>capacity lets see how it will effect our required values.
  1. table[c] has not been overriden yet in this current iteration, so it should be fine.
  2. table[c-weights[i]] may have been overriden in this current iteration and hence can’t be used in current iteration.
• To solve the problem in second case, we can change our inner loop to process in reverse direction c: capacity–>0, this will ensure whenever we change value in table[], we will not need it anymore in current iteration.

Code:

def solve_knapsack_dp_tabulation_optimized_space(profits, weights, capacity):
    table = [0]*(capacity+1)
    
    # If we consider only first weight, we will take it if its weight is less than capacity
    for c in range(capacity+1):
        if(weights[0] <= c):
            table[c] = profits[0]
    
    # Now consider rest by taking max of 1) current item can be included 2) current item is excluded
    for i in range(1, len(profits)):
        for c in range(capacity, -1, -1):
            if(weights[i] <= c):
                table[c] = max(table[c], profits[i] + table[c-weights[i]])
            else:
                table[c] = table[c]
    
    return table[capacity]


print("\nDP -> Iteration + Tabulation - Optimized Space Method :")
print(solve_knapsack_dp_tabulation_optimized_space([1, 6, 10, 16], [1, 2, 3, 5], 7))
print(solve_knapsack_dp_tabulation_optimized_space([1, 6, 10, 16], [1, 2, 3, 5], 6))

Output:

DP -> Iteration + Tabulation - Optimized Space Method :
22
17

Complexity:

• Time: O(N*C)
• Space: O(C)

2. Equal Subset Sum Partition

Problem:

3. Subset Sum

Problem:

4. Minimum Subset Sum Difference

Problem:

5. Count of Subset Sum

Problem:

6. Target Sum

Problem:

---

← Previous: Fibonacci Numbers Pattern

Next: Unbounded Knapsack Pattern →