Longest Palindromic Subsequence Pattern
Problems Following Palindromic Subsequence Pattern
1. Longest Palindromic Subsequence
Problem Statement:
Given a sequence, find the length of longest palindromic subsequence (LPS).
In Palindromic subsequence, elements read the same backword and forward.
A subsequence is a sequence that can be derived from anothe subsequence by deleting some or no elements without changing the order of remaining elements.
======= Examples: =======
Input: "abdbca"
Output: 5 => "abdba"
Input: "cddpd"
Output: 3 => "ddd"
Input: "pqr"
Output: 1 => any single char "p" or "q" or "r"
Brute-Force : Recursive Solution
- We can try all the subsequences of the given sequence.
- Start processing from the beginning and the end of the sequence. So now at any step, we have 2 options:
- If the element at the beginning and at the end are same, increment count by 2 and make recursive call for remaining sequence.
- If element at both end are not same, make two recursive calls for remainnig sequence skipping element from either end.
- If option-1 applies, it gives the length of LPS, otherwise the the length of LPS will be max of two recursive calls.
Code:
def find_lps_length_recursion(string):
start, end = 0, len(string) - 1
return find_lps_length_recursion_util(string, start, end)
def find_lps_length_recursion_util(string, start, end):
if (start > end):
return 0
if (start == end):
return 1
if (string[start] == string[end]):
return 2 + find_lps_length_recursion_util(string, start + 1, end - 1)
else:
skip_start_lps = find_lps_length_recursion_util(string, start + 1, end)
skip_end_lps = find_lps_length_recursion_util(string, start, end - 1)
return max(skip_start_lps, skip_end_lps)
print("Recursive Method :")
print(find_lps_length_recursion("abdbca"))
print(find_lps_length_recursion("cddpd"))
print(find_lps_length_recursion("pqr"))
Output:
Recursive Method :
5
3
1
Complexity:
- Time: O(2N) - Two recursive calls at max every time.
- Space: O(N) - To store the recursion stack. Max depth of recurstion stack is N.
DP : Recursion + Memoization (Top-Down) Solution
- We can use memoizaton to solve the recurring problem.
- The two changing values in our recursive function is start and end indexes.
- We can use 2-D array to store solution to our repeated subproblems.
- We can also use start + “|” + end as key to store in a hashmap.
Code:
def find_lps_length_dp_memoization(string):
n = len(string)
start, end = 0, n - 1
memory = [[None]*n for i in range(n)]
return find_lps_length_memoization_util(string, start, end, memory)
def find_lps_length_memoization_util(string, start, end, memory):
if (start > end):
return 0
if (start == end):
return 1
if (memory[start][end]):
return memory[start][end]
if (string[start] == string[end]):
memory[start][end] = 2 + find_lps_length_memoization_util(string, start + 1, end - 1, memory)
return memory[start][end]
skip_start_lps = find_lps_length_memoization_util(string, start + 1, end, memory)
skip_end_lps = find_lps_length_memoization_util(string, start, end - 1, memory)
memory[start][end] = max(skip_start_lps, skip_end_lps)
return memory[start][end]
print("\nDP -> Recursion + Memoization Method :")
print(find_lps_length_dp_memoization("abdbca"))
print(find_lps_length_dp_memoization("cddpd"))
print(find_lps_length_dp_memoization("pqr"))
Output:
DP -> Recursion + Memoization Method :
5
3
1
Complexity:
- Time: O(N2) - At max we can have N*N subproblems.
- Space: O(N2) - We need N*N to store results of sub-problems and N to store the recursion stack. Total is O(N2 + N), asymptotically O(N2).
DP : Iteration + Tabulation (Bottom-Up) Solution
- We can fill the table in bottom-up manner also.
- Start from the begining of the sequence and keep adding one element at a time.
- At every step we try all its subsequences, so for every start index and end index choose one option from below:
- If the element at start and end index mathces, LPS length will be 2 + LPS till start+1 and end-1.
- If they don’t match, take max LPS created by either skipping element at start or end.
Table Filling Formula:
if string[start] == string[end]:
table[start][end] = 2 + table[start+1][end-1]
else:
table[start][end] = max(table[start+1][end], table[start][end-1])
Tabulation:
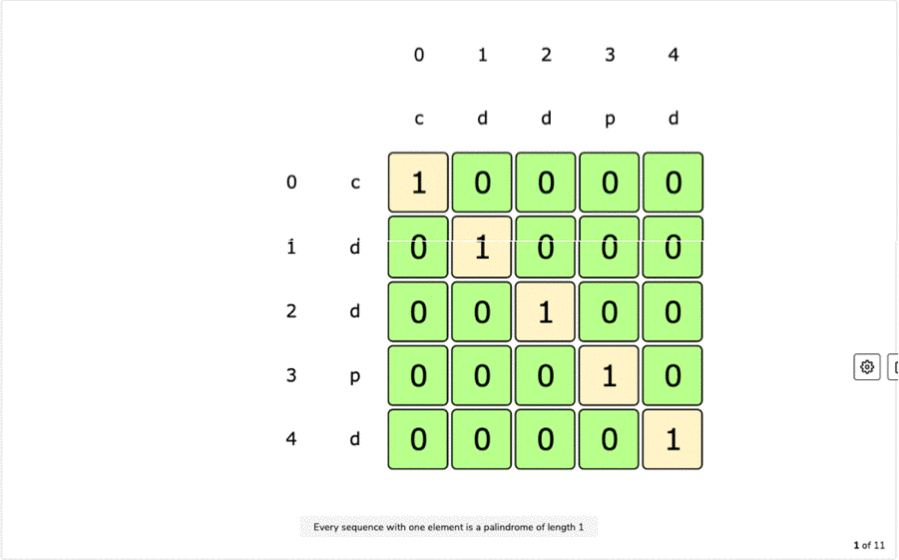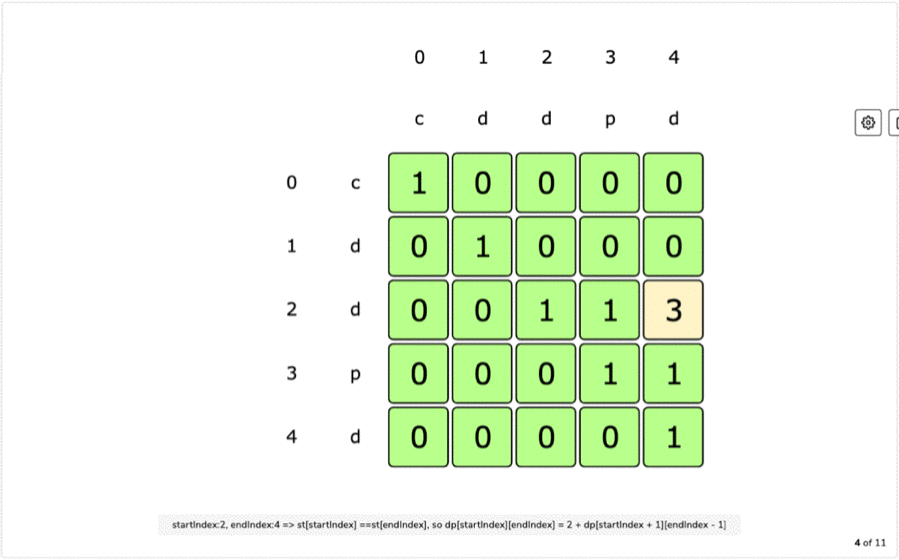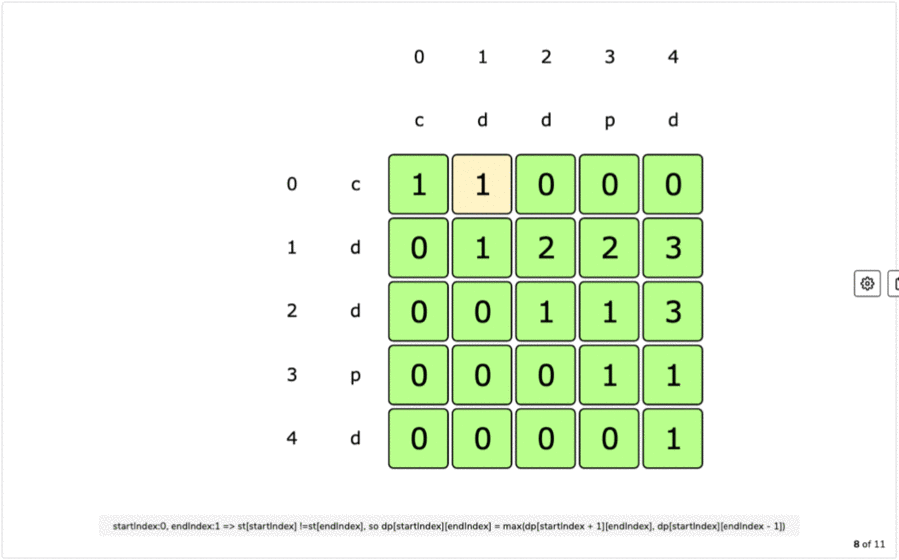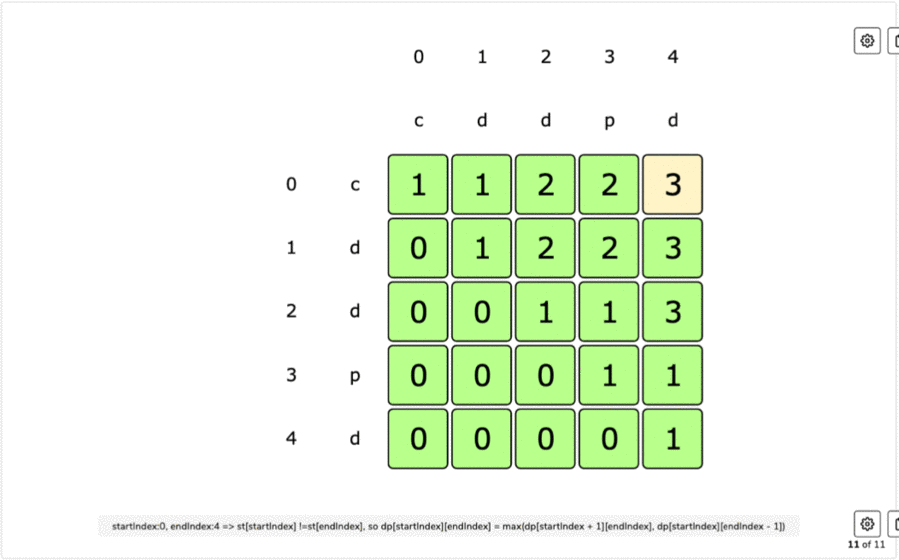
Final Table:

Code:
def find_lps_length_dp_tabulation(string):
n = len(string)
table = [[0] * n for _ in range(n)]
# When start and end indexes are equal palindrome length will be 1
for i in range(n):
table[i][i] = 1
# for filling table[start][end], we need to have table[start+1][end-1] ready
# Also, we need to fill only top right part of table coz bottom left will always be zero (start < end)
# Diaognal values will be 1, filled earlier
for start in range(n - 2, -1, -1):
for end in range(start + 1, n):
if (string[start] == string[end]):
table[start][end] = 2 + table[start + 1][end - 1]
else:
table[start][end] = max(table[start + 1][end], table[start][end - 1])
return table[0][n-1]
print("\nDP -> Iteration + Tabulation Method :")
print(find_lps_length_dp_tabulation("abdbca"))
print(find_lps_length_dp_tabulation("cddpd"))
print(find_lps_length_dp_tabulation("pqr"))
Output:
DP -> Iteration + Tabulation Method :
5
3
1
Complexity:
- Time: O(N2) - At max we can have N*N subproblems.
- Space: O(N2) - We need N*N to store results of sub-problems.
2. Longest Palindromic Substring
Problem Statement:
Given a string, find the length of its longest palindromic substring.
A substring is a continuous part of string and palindromic substring, elements read the same backword and forward.
======= Examples: =======
Input: "abdbca"
Output: 3 => "bdb"
Input: "cddpd"
Output: 3 => "dpd"
Input: "pqr"
Output: 1 => any single char "p" or "q" or "r"
Brute-Force : Recursive Solution
- This problem follows the Longest Palindromic Subsequence Pattern.
- Only difference is that in subsequence, characters can be non adjacent, but in substring all characters should be continuous.
- The brute-force way is to try all the substring of the given string.
- Start processing from the begining and the end of the string. Now at any step we have 2 options:
- If element at start and end are same, make a recursive call to check if remaining substring is also a palindrome. If it is then substring from start to end is a palindrome.
- Skip either from start and end to make two recursive calls for remaining substring, lps lenght will be max of both of these.
Code:
def find_lps_length_recursion(string):
start, end = 0, len(string) - 1
return find_lps_length_recursion_util(string, start, end)
def find_lps_length_recursion_util(string, start, end):
if (start > end):
return 0
if (start == end):
return 1
if (string[start] == string[end]):
remainingLength = end - start - 1
if (remainingLength == find_lps_length_recursion_util(string, start + 1, end - 1)):
return 2 + remainingLength
skip_start_lps = find_lps_length_recursion_util(string, start + 1, end)
skip_end_lps = find_lps_length_recursion_util(string, start, end - 1)
return max(skip_start_lps, skip_end_lps)
print("Recursive Method :")
print(find_lps_length_recursion("abdbca"))
print(find_lps_length_recursion("cddpd"))
print(find_lps_length_recursion("pqr"))
Output:
Recursive Method :
3
3
1
Complexity:
- Time: O(2N) - Two recursive calls at max every time.
- Space: O(N) - To store the recursion stack. Max depth of recurstion stack is N.
DP : Recursion + Memoization (Top-Down) Solution
- Similar to the Palindromic Subsequence Problem, we can use memoizaton to solve the recurring problem.
- The two changing values in our recursive function is start and end indexes.
- We can use 2-D array to store solution to our repeated subproblems.
- We can also use start + “|” + end as key to store in a hashmap.
Code:
def find_lps_length_dp_memoization(string):
n = len(string)
start, end = 0, n - 1
memory = [[None]*n for _ in range(n)]
return find_lps_length_dp_memoization_util(string, start, end, memory)
def find_lps_length_dp_memoization_util(string, start, end, memory):
if (start > end):
return 0
if (start == end):
return 1
if (memory[start][end]):
return memory[start][end]
if (string[start] == string[end]):
remainingLength = end - start - 1
if (remainingLength == find_lps_length_dp_memoization_util(string, start + 1, end - 1, memory)):
memory[start][end] = 2 + remainingLength
return memory[start][end]
skip_start_lps = find_lps_length_dp_memoization_util(string, start + 1, end, memory)
skip_end_lps = find_lps_length_dp_memoization_util(string, start, end - 1, memory)
memory[start][end] = max(skip_start_lps, skip_end_lps)
return memory[start][end]
print("\nDP -> Recursion + Memoization Method :")
print(find_lps_length_dp_memoization("abdbca"))
print(find_lps_length_dp_memoization("cddpd"))
print(find_lps_length_dp_memoization("pqr"))
Output:
DP -> Recursion + Memoization Method :
3
3
1
Complexity:
- Time: O(N2) - At max we can have N*N subproblems.
- Space: O(N2) - We need N*N to store results of sub-problems and N to store the recursion stack. Total is O(N2 + N), asymptotically O(N2).
DP : Iteration + Tabulation (Bottom-Up) Solution
- We can fill the table in bottom-up manner also.
- Start from the begining of the sequence and keep adding one element at a time.
- At every step we try all its substrings, so for every start index and end index need to check the following thing:
- If the element at start and end indexes are same, check if remaining substring start+1 to end-1 is also a palindrome.
Table Filling Formula:
if(string[start] == string[end]):
if( remaining string is of zero length or remaing string is a palindrome i.e. table[start+1][end-1] == True):
table[start][end] = True
Tabulation:

Final Table:
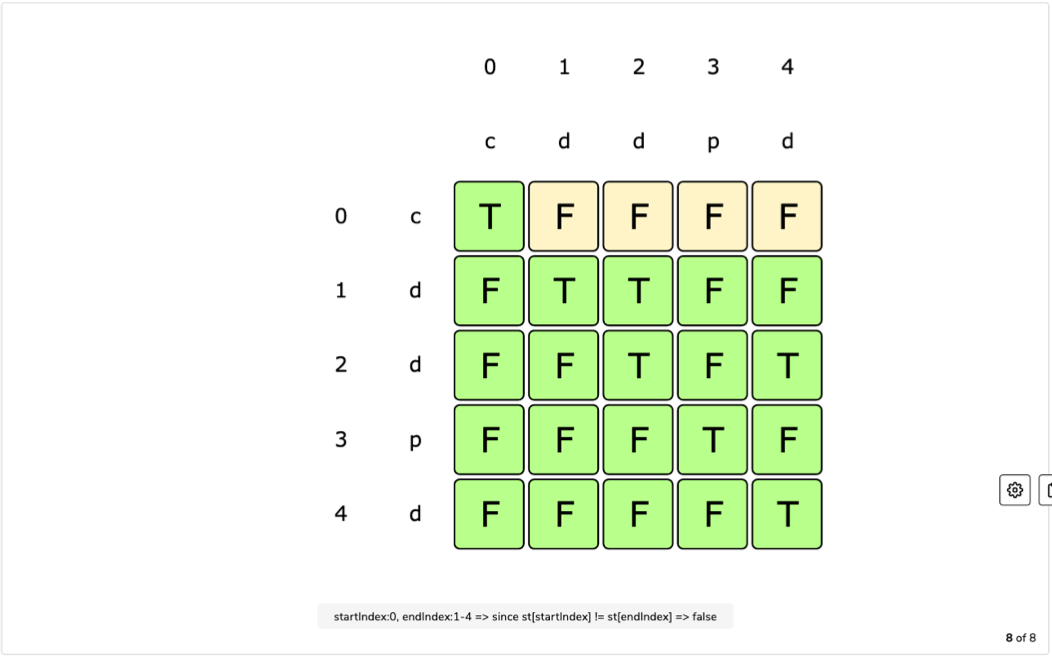
Code:
def find_lps_length_dp_tabulation(string):
n = len(string)
table = [[False] * n for _ in range(n)]
# Substring of length-1 will always be palindrome
for i in range(n):
table[i][i] = True
lps_length = 1
for start in range(n - 2, -1, -1):
for end in range(start + 1, n):
# If char at start and index is same
if (string[start] == string[end]):
# If remaining string is of zero length or it is a palindrome
if (end - start == 1 or table[start + 1][end - 1]):
table[start][end] = True
lps_length = max(lps_length, end - start + 1)
return lps_length
print("\nDP -> Iteration + Tabulation Method :")
print(find_lps_length_dp_tabulation("abdbca"))
print(find_lps_length_dp_tabulation("cddpd"))
print(find_lps_length_dp_tabulation("pqr"))
Output:
DP -> Iteration + Tabulation Method :
3
3
1
Complexity:
- Time: O(N2) - At max we can have N*N subproblems.
- Space: O(N2) - We need N*N to store results of sub-problems.
Manacher Algorithm:
- It is the linear time O(N) and best known algorithm for finding longest palindromic substring.
- But it is a non-trivial algorithm and don’t use dynamic programming.
- No one expects someone to come up with this algorithm in a 45-minutes interview.
3. Count of Palindromic Substrings
4. Minimum Deletions in a String to make it a Palindrome
5. Palindromic Partitioning
← Previous: Unbounded Knapsack Pattern
Next: Longest Common Substring Pattern →