Dynamic Programming Patterns
Dynamic Programming
- It is an algorithmic paradigm that solves a given complex problem by breaking it into subproblems and storing the results of subproblems to avoid computing the same results again.
- Utilizes the fact that the optimal solution to the overall problem depends on the optimal solutions to its subproblems.
- Example: Fibonacci numbers - We can calculate nth Fibonacci by below eqution
fib(n) = fib(n-1) + fib(n-2) for n > 1
- Here to solve the overall problem we broke it down to smaller subproblems.
Characteristics of Dynamic Programming
- Subproblems are smaller version of the original problem.
- Any problem has overlappping subproblems if finding its solution involves solving the same subproblem multiple times.
- Like Divide and Conquer, Dynamic Programming combines solutions to sub-problems.
- Dynamic Programming is mainly used when solutions of same subproblems are needed again and again.
- In dynamic programming, computed solutions to subproblems are stored in a table so that these don’t have to be recomputed.
- Dynamic Programming is not useful when there are no common (overlapping) subproblems because there is no point storing the solutions if they are not needed again.
- Binary Search is broken down into subproblems but it doesn’t have common subproblems, so no sense to store the solutions.

- Here we can see overlapping subproblems as fib(2) is evaluated twice and fib(1) evaluated thrice.
2. Optimal Substructure Property
-
Any problem has optimal substructure property if its overall optimal solution can be constructed from optimal solution of subproblems.
-
fib(n)= fib(n-1)+fib(n-2)- shows that overall problem of size n is reduced to subproblems of size n-1 and n-2. -
Example:- The Shortest Path problem has following optimal substructure property:
- If a node x lies in the shortest path from a source node u to destination node v.
- Then the shortest path from u to v is combination of shortest path from u to x and shortest path from x to v.
- The standard All Pair Shortest Path algorithms like Floyd–Warshall and Bellman–Ford are typical examples of Dynamic Programming.
-
But the Longest Path problem i.e. longest simple path (path without cycle) between two nodes doesn’t have the Optimal Substructure property.
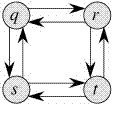
- There are two longest paths from q to t: q→r→t and q→s→t.
- Unlike shortest paths, these longest paths do not have the optimal substructure property.
- Example:- The longest path q→r→t is not a combination of longest path from q to r and longest path from r to t.
- Coz the longest path from q to r is q→s→t→r and the longest path from r to t is r→q→s→t.
Methods to Solve Dynamic Programming Problem
1. Recursion + Memoization (Top-Down Approach)
- Solve bigger problem by recursiverly finding the solution to smaller sub-problems.
- Whenever we solve a sub-problem we cache its result to avoid calling it multiple times.
- This technique of storing the results of already solved subproblems k/a Memoization.
2. Iteration + Tabulation (Bottom-Up Approach)
- Tabulation is opposite of Top-Down Approach and avoids recursion.
- In this we solve the problem bottom up (i.e by solving all the related subproblems first).
- This is typically done by filling an n-dimensional table.
- Based on the results in the table, the solution to the top/orignal problem is computed.
- Both Tabulated and Memoized store the solutions of subproblems.
- In Memoized version, table is filled on demand but in Tabulated version, starting from the first entry, all entries are filled one by one.
- Unlike the Tabulated version, all entries of the lookup table are not necessarily filled in Memoized version.
- Example:- Memoized solutionof the LCS problem doesn’t necessarily fill all entries.
Patterns to be studied:
- Fibonacci Numbers Pattern
- 0/1 Knapsack Pattern
- Unbounded Knapsack Pattern
- Palindromic Subsequence Pattern
- Longest Common Substring Pattern
Next: Fibonacci Numbers Pattern →