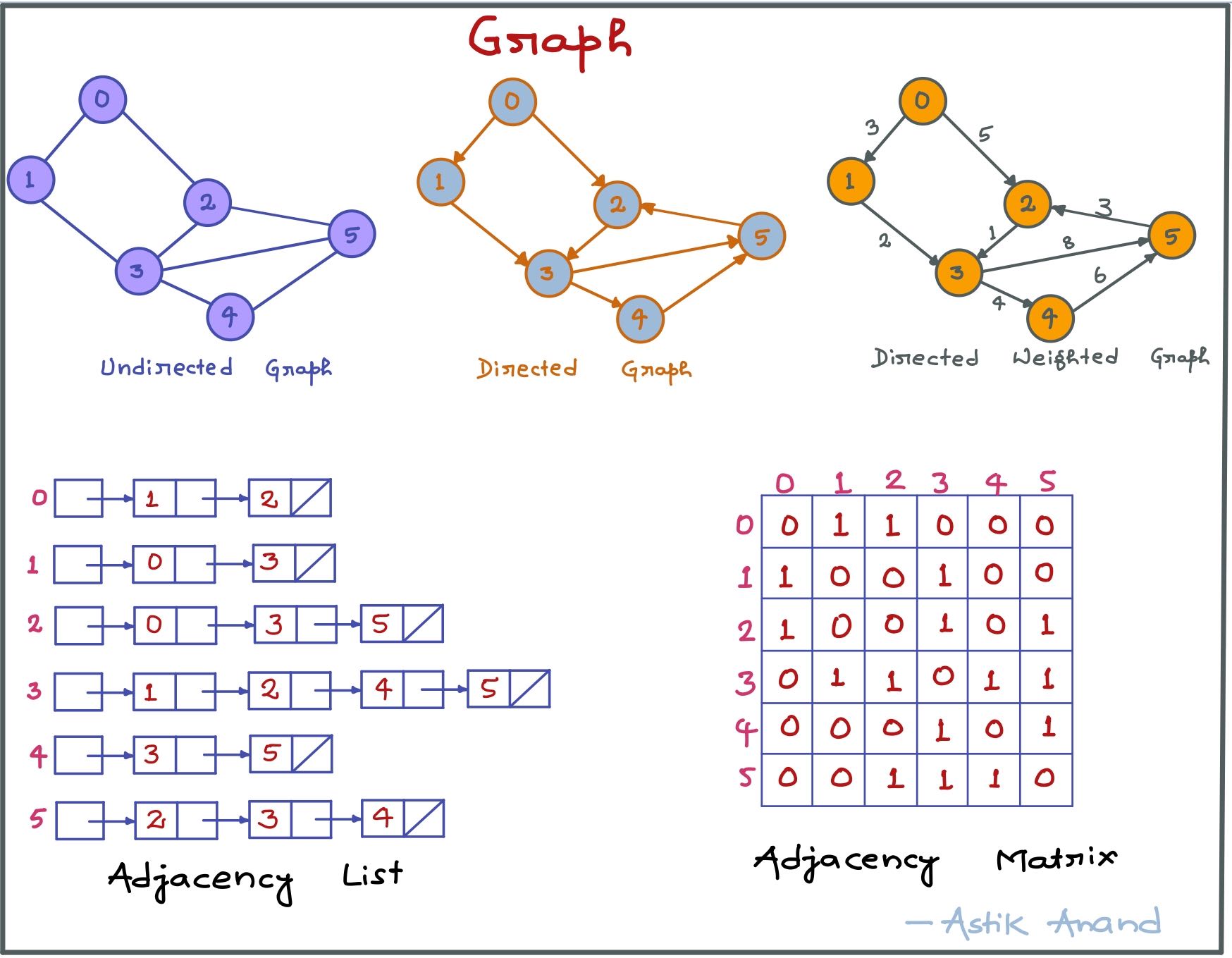
Home techblogs data-structures graph

Graph

What is Graph ?

Graph is a data structure that consists of following two components:

Representation

1. Adjacency Matrix
2. Adjacency List
Implementation
from collections import defaultdict

class Graph:
    def __init__(self):
        self.graph = defaultdict(list)
    
    def add_edge(self, u, v):
        self.graph[u].append(v)
        self.graph[v].append(u)     # If undirected
    
    def print_graph(self):
        # print the vertex
        for vertex in self.graph:
            print("[{}]".format(vertex), end="")
            # print the connected_vertices to this vertex
            for connected_vertex in self.graph[vertex]:
                print("-->{}".format(connected_vertex), end="")
            print()



print("Example-1: Graph Representation")
g = Graph()
g.add_edge(0, 1)
g.add_edge(0, 2)
g.add_edge(1, 3)
g.add_edge(2, 3)
g.add_edge(2, 5)
g.add_edge(3, 4)
g.add_edge(3, 5)
g.add_edge(4, 5)
g.print_graph()

Output:

graph_representation_output


Applications of Graph

Graphs are used to represent many real-life applications:



Algo-1: Breadth First Seach (BFS)

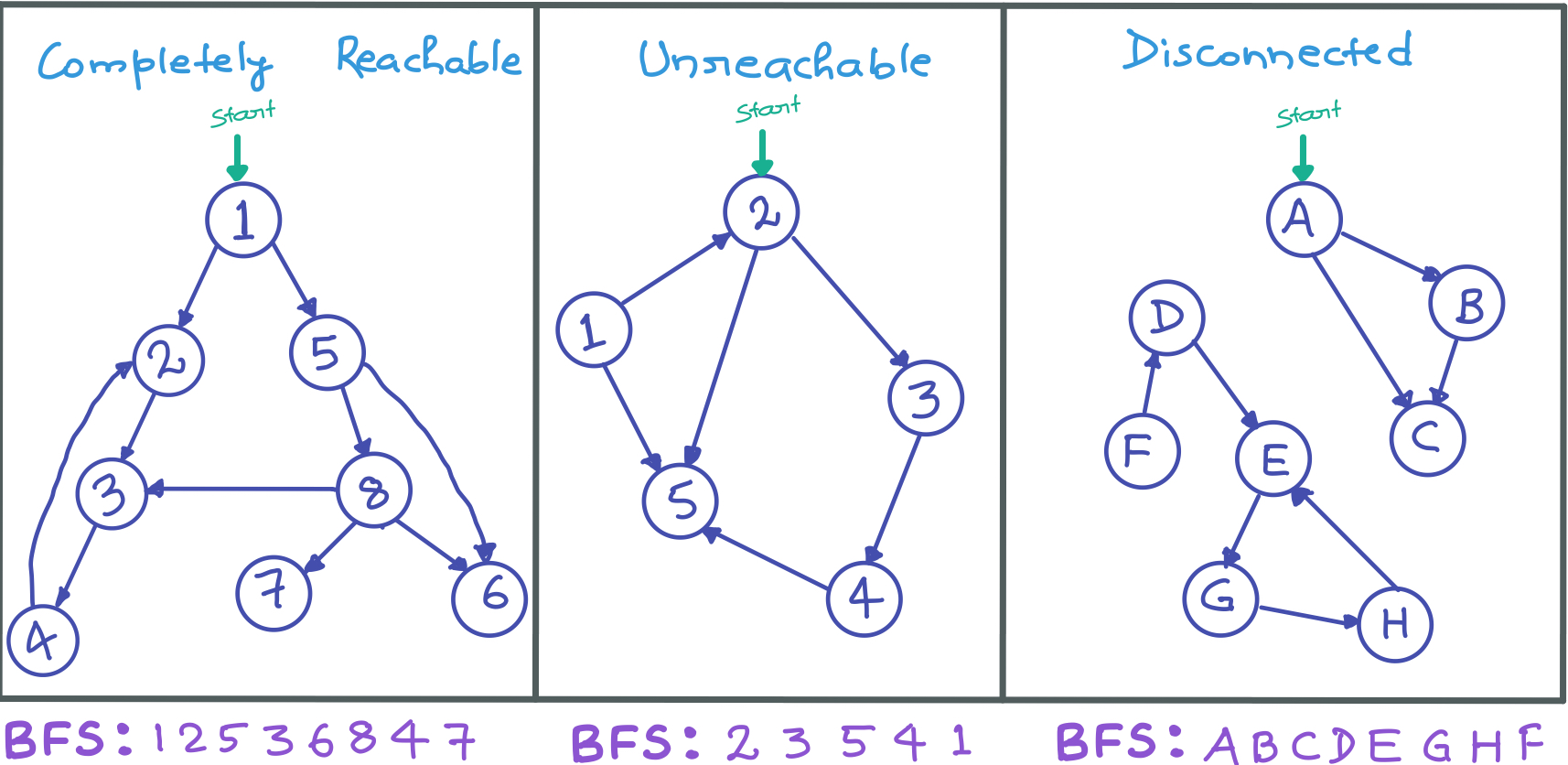
What is BFS ?

Approach or Algorithm:
  1. Start with the given start_vertex, take a queue and enqueue the start_vertex to it and mark it as visited.
  2. While queue is not empty take out the current_vertex from queue and print it:
    • See all the connected vertices to current_vertex:
      • If any connected_vertex is not visited enqueue to the queue and mark it visited.
  3. Check if any unvisited vertex (case of UNREACHABLE or DISCONNECTED graphs):
    • Call the function again from unvisited vertex
Implementation:
class Graph:
    def __init__(self):
        self.graph = {}
    
    def add_vertex(self, vertex):
        if vertex not in self.graph:
            self.graph[vertex] = []
    
    def add_edge(self, u, v):
        self.add_vertex(u)
        self.add_vertex(v)
        self.graph[u].append(v)

    def unvisited(self, visited):
        for vertex in visited:
            if(visited[vertex] is False):
                return vertex
        return None

    def bfs_traversal_util(self, start_vertex, visited):
        # Take a queue and enqueue the start_vertex and mark it as visited
        queue = []
        queue.append(start_vertex)
        visited[start_vertex] = True

        # Dequeue out the current_vertex from queue and print it
        while(queue):
            current_vertex= queue.pop(0)
            print("{}".format(current_vertex), end=" ")
            # See all the connected vertices to current_vertex
            for connected_vertex in self.graph[current_vertex]:
                # If any connected_vertex is not visited enqueue to the queue and mark it visited
                if(visited[connected_vertex] is False):
                    queue.append(connected_vertex)
                    visited[connected_vertex] = True
 
    def bfs_traversal(self, start_vertex):
        # Mark every every vertex as unvisited
        visited = {}
        for vertex in self.graph:
            visited[vertex] = False
        
        # Call the bfs_traversal_util with start_vertex
        self.bfs_traversal_util(start_vertex, visited)

        # Check if there is still any unvisited vertex
        # Only when graph is UNREACHABLE or DISCONNECTED below lines will be executed
        while(self.unvisited(visited) is not None):
            # Call the bfs_traversal_util from the unvisited vertex
            self.bfs_traversal_util(self.unvisited(visited), visited)
        print()



print("Example-1: BFS Traversal of Graph from vertex-1:")
g = Graph()
g.add_edge(1, 2)
g.add_edge(2, 3)
g.add_edge(3, 4)
g.add_edge(4, 2)
g.add_edge(1, 5)
g.add_edge(5, 6)
g.add_edge(5, 8)
g.add_edge(8, 3)
g.add_edge(8, 6)
g.add_edge(8, 7)
g.bfs_traversal(1)

print("Example-2: BFS Traversal of Graph from vertex-2:")
g = Graph()
g.add_edge(1, 2)
g.add_edge(1, 5)
g.add_edge(2, 3)
g.add_edge(2, 5)
g.add_edge(3, 4)
g.add_edge(4, 5)
g.bfs_traversal(2)

print("Example-3: BFS Traversal of Graph from vertex-A:")
g = Graph()
g.add_edge("A", "B")
g.add_edge("A", "C")
g.add_edge("B", "C")
g.add_edge("D", "E")
g.add_edge("E", "G")
g.add_edge("F", "D")
g.add_edge("G", "H")
g.add_edge("H", "E")
g.bfs_traversal("A")

Output:

breadth_first_search_output

Complexity:

Applications of BFS



Algo-2: Depth First Search (DFS)

What is DFS ?

Algorithm
  1. Mark the given vertex as visited and print it.
  2. See all the connected vertices to current_vertex:
    • If any connected_vertex is not visited make the recursive call from that vertex.
  3. Check if any unvisited vertex (case of UNREACHABLE or DISCONNECTED graphs):
    • Call the function again from unvisited vertex.
Recursive Implementation
class Graph:
    def __init__(self):
        self.graph = {}
    

    def add_vertex(self, vertex):
        if vertex not in self.graph:
            self.graph[vertex] = []
    

    def add_edge(self, u, v):
        self.add_vertex(u)
        self.add_vertex(v)
        self.graph[u].append(v)


    def unvisited(self, visited):
        for vertex in visited:
            if(visited[vertex] is False):
                return vertex
        return None


    def dfs_traversal_recursive_util(self, vertex, visited):
        visited[vertex] = True
        print("{}".format(vertex), end=" ")

        # See all the connected vertices to vertex and make recursive call from 
        # the vertex not already visited
        for connected_vertex in self.graph[vertex]:
            if(visited[connected_vertex] is False):
                self.dfs_traversal_recursive_util(connected_vertex, visited)
    

    def dfs_traversal_recursive(self, start_vertex):
         # Mark every every vertex as unvisited
        visited = {}
        for vertex in self.graph:
            visited[vertex] = False
        
        # Call the dfs_traversal_recursive_util with start_vertex
        self.dfs_traversal_recursive_util(start_vertex, visited)

        # Check if there is still any unvisited vertex
        # Only when graph is UNREACHABLE or DISCONNECTED below lines will be executed
        while(self.unvisited(visited) is not None):
            # Call the dfs_traversal_recursive_util from the unvisited vertex
            self.dfs_traversal_recursive_util(self.unvisited(visited), visited)
        print()



print("Example-1: DFS Traversal of Graph (Recursive) from vertex-1:")
g = Graph()
g.add_edge(1, 2)
g.add_edge(2, 3)
g.add_edge(3, 4)
g.add_edge(4, 2)
g.add_edge(1, 5)
g.add_edge(5, 6)
g.add_edge(5, 8)
g.add_edge(8, 3)
g.add_edge(8, 6)
g.add_edge(8, 7)
g.dfs_traversal_recursive(1)

print("Example-2: DFS Traversal of Graph (Recursive) from vertex-2:")
g = Graph()
g.add_edge(1, 2)
g.add_edge(1, 5)
g.add_edge(2, 3)
g.add_edge(2, 5)
g.add_edge(3, 4)
g.add_edge(4, 5)
g.dfs_traversal_recursive(2)

print("Example-3: DFS Traversal of Graph (Recursive) from vertex-A:")
g = Graph()
g.add_edge("A", "B")
g.add_edge("A", "C")
g.add_edge("B", "C")
g.add_edge("D", "E")
g.add_edge("E", "G")
g.add_edge("F", "D")
g.add_edge("G", "H")
g.add_edge("H", "E")
g.dfs_traversal_recursive("A")

Output:

depth_first_search_recursive_output

Complexity:

Applications of DFS

Standard Graph Algorithms and Problems

1. Detect Cycle in Undirected Graph***

Problem:

Given a undirected graph, check whether the graph contains a cycle or not.

Approach:
Implementation:
class Graph:
    def __init__(self):
        self.graph = {}


    def add_vertex(self, vertex):
        if vertex not in self.graph:
            self.graph[vertex] = []
    

    def add_edge(self, u, v):
        self.add_vertex(u)
        self.add_vertex(v)
        self.graph[u].append(v)
        self.graph[v].append(u)


    def unvisited(self, visited):
        for vertex in visited:
            if(visited[vertex] == False):
                return vertex
        return None


    def detect_cycle_undirected_graph_util(self, current_vertex, parent, visited):
        # Mark the current_vertex as visited
        visited[current_vertex] = True

        # See the connected vertices to current_vertex one by one
        for connected_vertex in self.graph[current_vertex]:
            # If connected_vertex is not visited then make recursive call from the connected_vertex
            # with current_vertex as parent and return True if it returns True.
            if(visited[connected_vertex] == False):
                if(self.detect_cycle_undirected_graph_util(connected_vertex, current_vertex, visited) == True):
                    return True
            # Else if connected_vertex is already visited and it is not parent then cycle found return True.
            elif(connected_vertex != parent):
                print("Cycle Exists coz of {} ----- {}".format(current_vertex, connected_vertex))
                return True
        
        # Once the current_vertex is processed return False to show that 
        # cycle was not found while processing this current_vertex.
        return False


    def detect_cycle_undirected_graph(self, start_vertex):
        # Mark every every vertex as unvisited initially
        visited = {}
        for vertex in self.graph:
            visited[vertex] = False

        # Call the detect_cycle_undirected_graph_util with start_vertex
        cycle_exists = self.detect_cycle_undirected_graph_util(start_vertex, None, visited)

        # Check if there is still any unvisited vertex and cycle still not found
        # Only when graph is DISCONNECTED below lines will be executed
        while(self.unvisited(visited) is not None and cycle_exists == False):
            # Call the detect_cycle_undirected_graph_util from the unvisited vertex
            cycle_exists = self.detect_cycle_undirected_graph_util(self.unvisited(visited), None, visited)

        if(not cycle_exists):
            print("Cycle doesn't exist!")


print("Example-1: Detect Cycle in Undirected Graph:")
g = Graph()
g.add_edge(1, 2)
g.add_edge(2, 3)
g.add_edge(3, 4)
g.add_edge(3, 5)
g.add_edge(4, 5)
g.detect_cycle_undirected_graph(1)

print("\nExample-2: Detect Cycle in Undirected Graph:")
g = Graph()
g.add_edge(1, 2)
g.add_edge(2, 3)
g.add_edge(3, 4)
g.add_edge(3, 5)
g.detect_cycle_undirected_graph(1)

print("\nExample-3: Detect Cycle in Undirected Graph:")
g = Graph()
g.add_edge("A", "B")
g.add_edge("B", "C")
g.add_edge("D", "E")
g.add_edge("D", "F")
g.add_edge("E", "G")
g.add_edge("E", "H")
g.add_edge("G", "H")
g.detect_cycle_undirected_graph("A")

Output:

detect_cycle_undirected_graph_output

Complexity:



2. Detect Cycle in Directed Graph***

Problem:

Given a directed graph, check whether the graph contains a cycle or not.

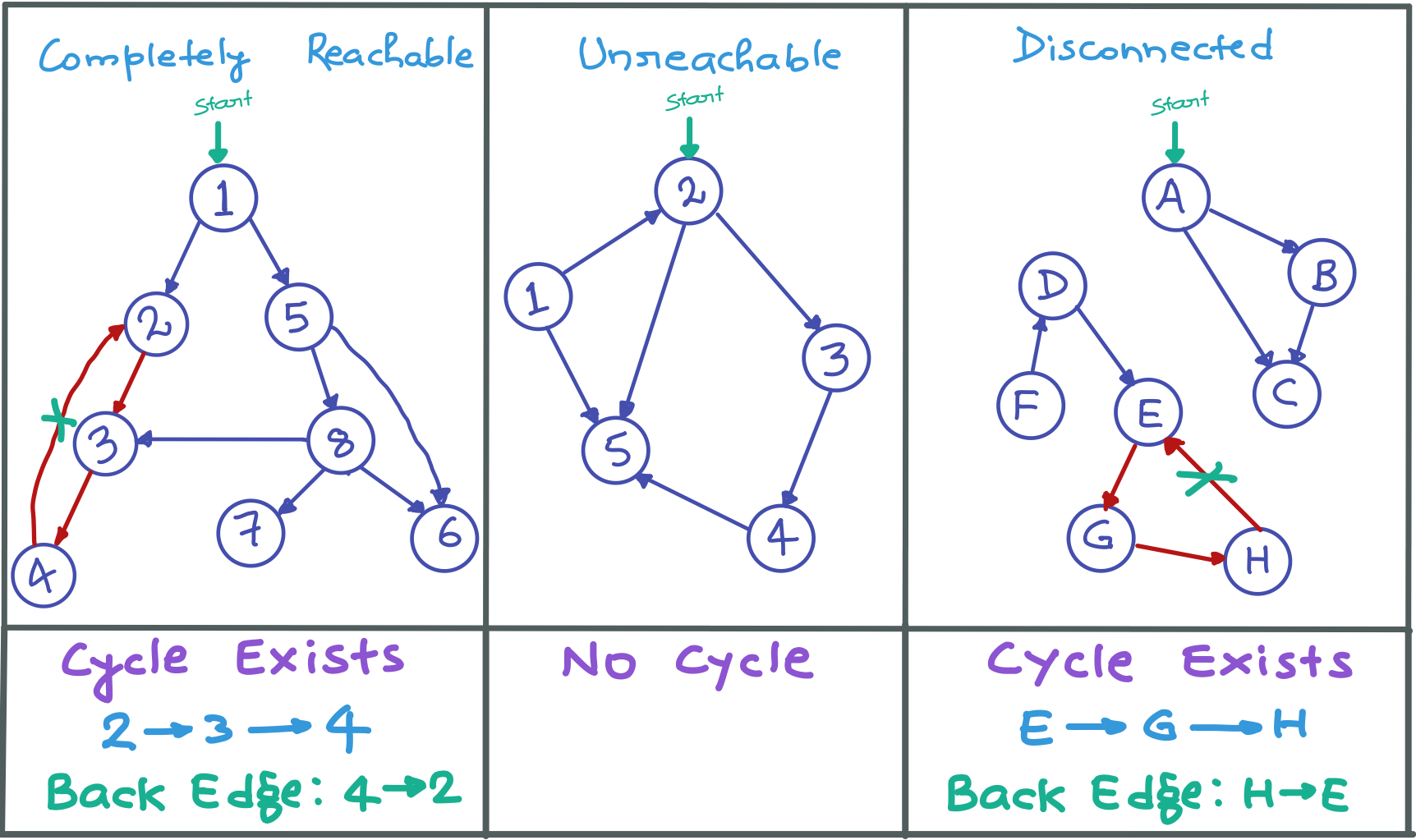
Important Facts:
Approach:
Implementation
class Graph:
    def __init__(self):
        self.graph = {}
    

    def add_vertex(self, vertex):
        if vertex not in self.graph:
            self.graph[vertex] = []
    

    def add_edge(self, u, v):
        self.add_vertex(u)
        self.add_vertex(v)
        self.graph[u].append(v)
    

    def unvisited(self, visited):
        for vertex in visited:
            if(visited[vertex] == "white"):
                return vertex
        return None

    
    def detect_cycle_directed_graph_util(self, current_vertex, color):
        # Mark the current_vertex as "gray" i.e. processing
        color[current_vertex] = "gray"

        # See the connected vertices to current_vertex one by one
        for connected_vertex in self.graph[current_vertex]:
            # If connected_vertex is "white" i.e. still to be processed then 
            # make recursive call from the connected_vertex
            # and return True if it returns True                                                   
            if(color[connected_vertex] == "white"):
                if(self.detect_cycle_directed_graph_util(connected_vertex, color) == True):
                    return True
            # Else if connected_vertex is "gray" i.e. in processing then we have found the cycle return True
            elif(color[connected_vertex] == "gray"):
                print("Cycle Exists coz of {} -----> {}". format(current_vertex, connected_vertex))
                return True
        
        # If reaches here that means processing of current vertex is done, mark it black
        # return False to show that cycle was not found while processing this current_vertex
        color[current_vertex] = "black"
        return False
    

    def detect_cycle_directed_graph(self, start_vertex):
        # Mark every every vertex as "white" i.e. still to be processed
        color = {}
        for vertex in self.graph:
            color[vertex] = "white"
        
        # Call the detect_cycle_directed_graph_util with start_vertex
        cycle_exists = self.detect_cycle_directed_graph_util(start_vertex, color)

        # Check if there is still any "white” vertex and cycle still not found
        # Only when graph is UNREACHABLE or DISCONNECTED below lines will be executed
        while(self.unvisited(color) is not None and cycle_exists == False):
            # Call the detect_cycle_directed_graph_util from the "white" vertex
            cycle_exists = self.detect_cycle_directed_graph_util(self.unvisited(color), color)
        
        if(not cycle_exists):
            print("Cycle doesn't exist!")
        


print("Example-1: Detect Cycle in Directed Graph:")
g = Graph()
g.add_edge(1, 2)
g.add_edge(2, 3)
g.add_edge(3, 4)
g.add_edge(4, 2)
g.add_edge(1, 5)
g.add_edge(5, 6)
g.add_edge(5, 8)
g.add_edge(8, 3)
g.add_edge(8, 6)
g.add_edge(8, 7)
g.detect_cycle_directed_graph(1)

print("\nExample-2: Detect Cycle in Directed Graph:")
g = Graph()
g.add_edge(1, 2)
g.add_edge(1, 5)
g.add_edge(2, 3)
g.add_edge(2, 5)
g.add_edge(3, 4)
g.add_edge(4, 5)
g.detect_cycle_directed_graph(1)

print("\nExample-3: Detect Cycle in Directed Graph:")
g = Graph()
g.add_edge("A", "B")
g.add_edge("A", "C")
g.add_edge("B", "C")
g.add_edge("D", "E")
g.add_edge("E", "G")
g.add_edge("F", "D")
g.add_edge("G", "H")
g.add_edge("H", "E")
g.detect_cycle_directed_graph("A")

Output:

detect_cycle_directed_graph_output

Complexity:



3. Topological Sorting***

What is Topological Sorting:

Topological sorting for Directed Acyclic Graph (DAG) is a linear ordering of vertices such that for every directed edge uv, vertex u comes before v in the ordering.

Important Facts:
Approach:
  1. Mark the given vertex as visited.
  2. See all the connected vertices to current_vertex one by one:
    • If connected_vertex is not already visited then make recursive call from the connected_vertex.
  3. Once processing of current_vertex is done push it to result_stack.
  4. Check if any unvisited vertex still (case of UNREACHABLE or DISCONNECTED graphs):
    • Call the function again from unvisited vertex.
  5. Print the result_stack in reverse order.
Implementation
class Graph:
    def __init__(self):
        self.graph = {}
    

    def add_vertex(self, vertex):
        if vertex not in self.graph:
            self.graph[vertex] = []
    

    def add_edge(self, u, v):
        self.add_vertex(u)
        self.add_vertex(v)
        self.graph[u].append(v)


    def unvisited(self, visited):
        for vertex in visited:
            if(visited[vertex] is False):
                return vertex
        return None


    def topological_sort_util(self, current_vertex, visited, result_stack):
        # Mark the current_vertex as visited
        visited[current_vertex] = True

        # See all the connected vertices to current_vertex one by one
        for connected_vertex in self.graph[current_vertex]:
            # If connected_vertex is not already visited then make recursive call from the connected_vertex
            if(visited[connected_vertex] is False):
                self.topological_sort_util(connected_vertex, visited, result_stack)
        
        # Once processing of current_vertex is done push it to result_stack
        result_stack.append(current_vertex)


    def topological_sort(self, start_vertex):
         # Mark every every vertex as unvisited
        visited = {}
        for vertex in self.graph:
            visited[vertex] = False
        
        # Take a result_stack to store the result
        result_stack = []
        
        # Call the topological_sort_util with start_vertex
        self.topological_sort_util(start_vertex, visited, result_stack)

        # Check if there is still any unvisited vertex
        # Only when graph is UNREACHABLE or DISCONNECTED below lines will be executed
        while(self.unvisited(visited) is not None):
            # Call the topological_sort_util from the unvisited vertex
            self.topological_sort_util(self.unvisited(visited), visited, result_stack)
        
        # print the result_stack in reverse order
        result_stack.reverse()
        for vertex in result_stack:
            print("{} ".format(vertex), end="")
        print()



print("Example-1: Topological Sorting from vertex-1:")
g = Graph()
g.add_edge(1, 2)
g.add_edge(2, 3)
g.add_edge(3, 4)
g.add_edge(1, 5)
g.add_edge(5, 6)
g.add_edge(5, 8)
g.add_edge(8, 3)
g.add_edge(8, 6)
g.add_edge(8, 7)
g.topological_sort(1)

print("\nExample-2: Topological Sorting from vertex-6:")
g = Graph()
g.add_edge(3, 4)
g.add_edge(4, 2)
g.add_edge(5, 1)
g.add_edge(5, 2)
g.add_edge(6, 1)
g.add_edge(6, 3)
g.topological_sort(6)

print("\nExample-3: Topological Sorting from vertex-A:")
g = Graph()
g.add_edge("A", "B")
g.add_edge("A", "C")
g.add_edge("B", "C")
g.add_edge("D", "E")
g.add_edge("E", "G")
g.add_edge("F", "D")
g.add_edge("G", "H")
g.topological_sort("A")

Output:

topological_sorting-output

Complexity:

Applications of Topological Sorting



4. Prim’s Minimum Spanning Tree (MST) - Greedy***

What is Minimum Spanning Tree?

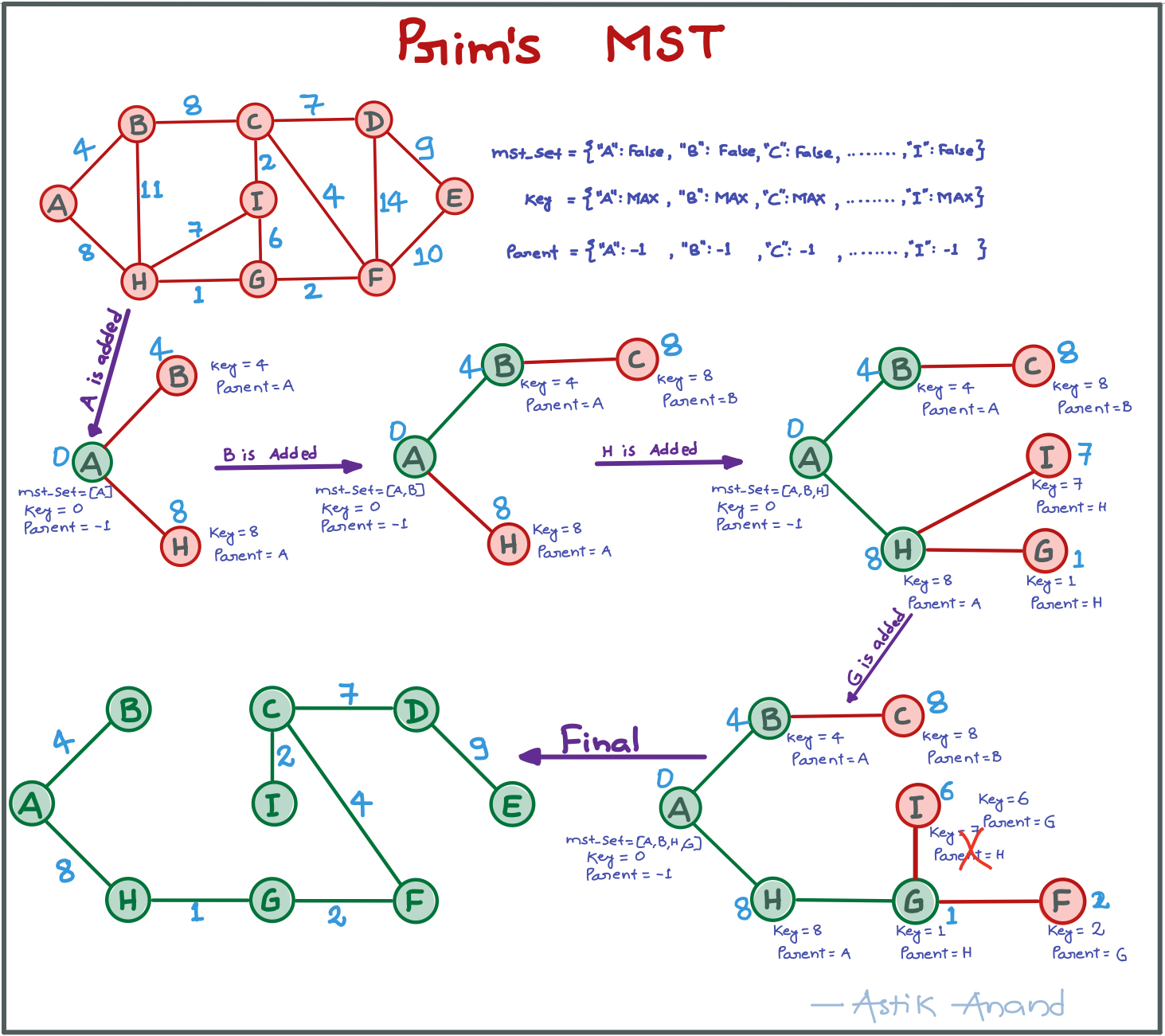
prim_mst

Important Facts:
Approach:
  1. Initially, set mst_set of every vertex as False, key of every vertex as “MAX” and parent of every vertex as ”-“.
  2. Set the key[start_vertex] = 0 and min_vertex = start_vertex :- from this vertex we will start the MST.
  3. While min_vertex is not None:
    • Add the min_vertex to the mst_set.
    • See all the connected vertices to min_vertex one by one. If the connected_vertex is not in mst_set and also weight of the connected_vertex < key[connected vertex],then update the key of connected vertex and also it’s parent to be the min_vertex
    • Again call the min_vertex to get new min_vertex with updated mst_set and key.
  4. Print the edges and their respective weights using parent and key dicts.
Implementation:
import sys

class Graph:
    def __init__(self):
        self.graph = {}
    

    def add_vertex(self, vertex):
        if vertex not in self.graph:
            self.graph[vertex] = []
    

    def add_edge(self, u, v, w):
        self.add_vertex(u)
        self.add_vertex(v)
        self.graph[u].append((v, w))
        self.graph[v].append((u, w))
    

    def get_min_key_vertex_not_in_mst(self, mst_set, key):
        min_key = sys.maxsize
        min_vertex = None
        for k in key:
            if(key[k] < min_key and mst_set[k] == False):
                min_key = key[k]
                min_vertex = k
        
        return min_vertex
                
    

    def prims_mst(self, start_vertex):
        # Initially, set mst_set of every vertex as False, 
        # key of every vertex as "MAX" and parent of every vertex as "-".
        mst_set = {}; key = {}; parent = {}
        for vertex in self.graph:
            mst_set[vertex] = False
            key[vertex] = sys.maxsize
            parent[vertex] = "-"
        
        # Set the key[start_vertex] = 0 and min_vertex = start_vertex : 
        # From this vertex we will start the MST
        key[start_vertex] = 0
        min_vertex = start_vertex

        while(min_vertex is not None):
            # Add the min_vertex to the mst_set
            mst_set[min_vertex] = True

            # See all the connected vertices to min_vertex one by one
            for connected_vertex in self.graph[min_vertex]:
                con_vertex = connected_vertex[0]
                con_vertex_weight = connected_vertex[1]
                # If the connected_vertex is not in mst_set and also 
                # weight of the connected_vertex < key[connected vertex],
                # then update the key of connected vertex and also it's parent to be the min_vertex
                if(mst_set[con_vertex] == False and con_vertex_weight < key[con_vertex]):
                    key[con_vertex] = con_vertex_weight
                    parent[con_vertex] = min_vertex
            
            # Again call the function to get new min_vertex with updated mst_set and key
            min_vertex = self.get_min_key_vertex_not_in_mst(mst_set, key)
        

        # Print the edges and their respective weights using parent and key dicts.
        ordered_parent = sorted(parent.items(), key=lambda k: (k[1]))
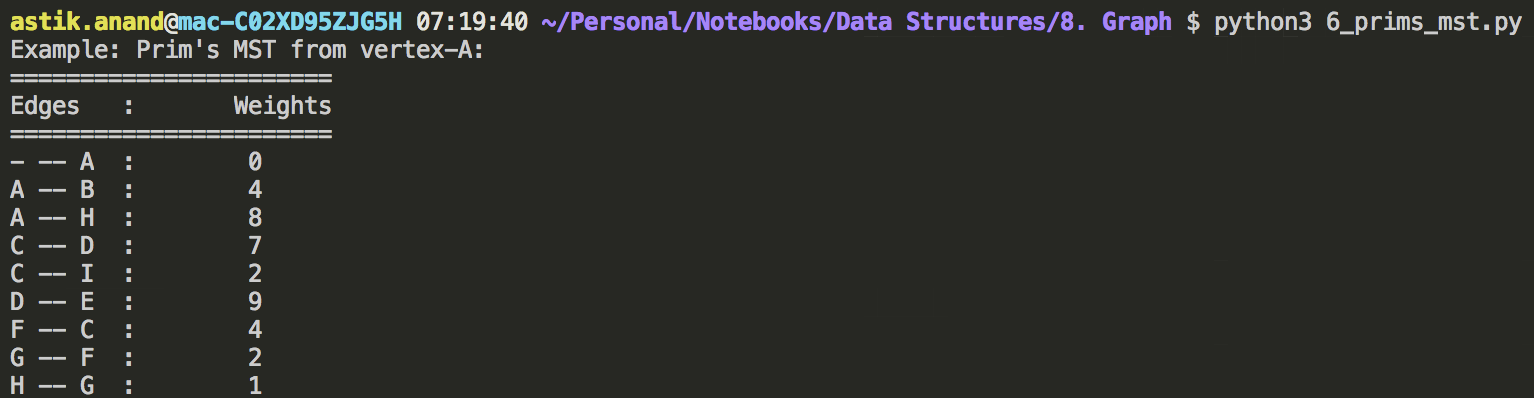
        print("="*23 + "\nEdges\t:\tWeights\n" + "="*23)
        for vertex, parent_vertex in ordered_parent:
            print("{} -- {} \t:\t {}".format(parent_vertex, vertex, key[vertex]))
        


print("Example: Prim's MST from vertex-A:")
g = Graph()
g.add_edge("A", "B", 4)
g.add_edge("A", "H", 8)
g.add_edge("B", "C", 8)
g.add_edge("B", "H", 11)
g.add_edge("C", "D", 7)
g.add_edge("C", "F", 4)
g.add_edge("C", "I", 2)
g.add_edge("D", "E", 9)
g.add_edge("D", "F", 14)
g.add_edge("E", "F", 10)
g.add_edge("F", "G", 2)
g.add_edge("G", "H", 1)
g.add_edge("G", "I", 6)
g.add_edge("H", "I", 7)
g.prims_mst("A")

Output:

prim_mst_output

Complexity:

Applications of MST



5. Dijkstra’s Shortest Path Algorithm - Greedy***

Problem:

Given a graph and a source vertex in the graph, find shortest paths from source to all vertices in the given graph.

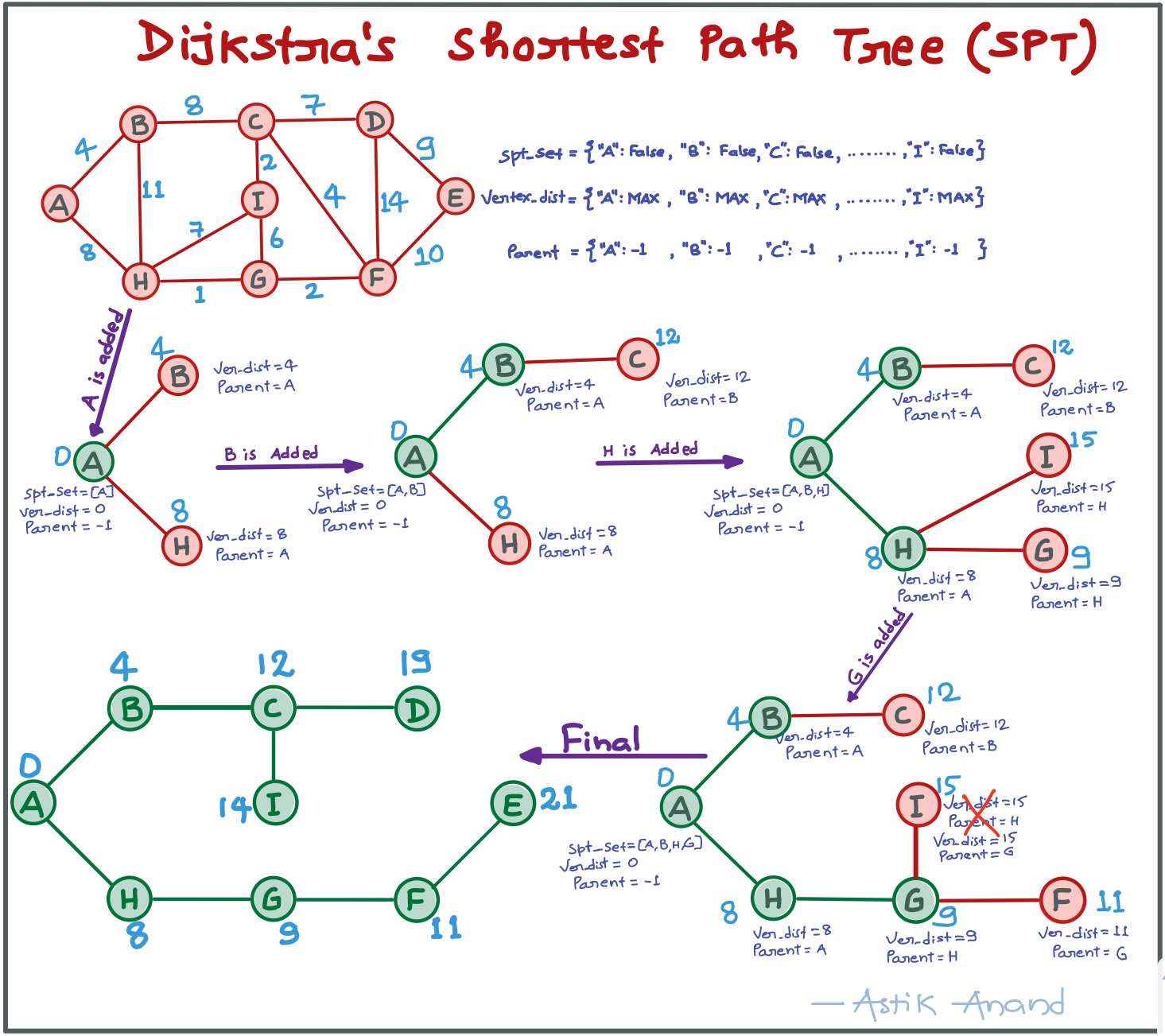
dijkstra_shortest_path

Important Facts:
Approach:
  1. Initially, set spt_set of every vertex as False, vertex_distance of every vertex as “MAX” and parent of every vertex as ”-“.
  2. Set the key[start_vertex] = 0 and min_vertex = start_vertex :- from this vertex we will start the MST.
  3. Set the vertex_distance[start_vertex] = 0 and min_distant_vertex = start_vertex :- From this vertex we will start the SPT.
  4. While min_distant_vertex is not None:
    • Add the min_distant_vertex to the spt_set.
    • See all the connected vertices to min_distant_vertex one by one. If the connected_vertex is not in spt_set and also weight of connected_vertex + vertex_distance[min_distant_vertex] < vertex_distance[connected vertex], then update the vertex_distance of connected_vertex and also it’s parent to be the min_distant_vertex.
    • Again call the function to get new min_distant_vertex with updated spt_set and vertex_distance.
  5. Print the Vertices and their respective distances from source and Reach by using parent and vertex_distance dicts.
Implementation
import sys

class Graph:
    def __init__(self):
        self.graph = {}
    

    def add_vertex(self, vertex):
        if vertex not in self.graph:
            self.graph[vertex] = []
    

    def add_edge(self, u, v, w):
        self.add_vertex(u)
        self.add_vertex(v)
        self.graph[u].append((v, w))
        self.graph[v].append((u, w))
    

    def get_min_distant_vertex_not_in_spt(self, spt_set, vertex_distance):
        min_vertex_distance = sys.maxsize
        min_distant_vertex = None
        for v in vertex_distance:
            if(vertex_distance[v] < min_vertex_distance and spt_set[v] == False):
                min_vertex_distance = vertex_distance[v]
                min_distant_vertex = v
        
        return min_distant_vertex
                
    

    def dijkstras_spt(self, start_vertex):
        # Initially, set spt_set of every vertex as False, 
        # vertex_distance of every vertex as "MAX" and parent of every vertex as "-".
        spt_set = {}; vertex_distance = {}; parent = {}
        for vertex in self.graph:
            spt_set[vertex] = False
            vertex_distance[vertex] = sys.maxsize
            parent[vertex] = "-"
        
        # Set the vertex_distance[start_vertex] = 0 and min_distant_vertex = start_vertex :- 
        # From this vertex we will start the SPT.
        vertex_distance[start_vertex] = 0
        min_distant_vertex = start_vertex

        while(min_distant_vertex is not None):
            # Add the min_distant_vertex to the spt_set
            spt_set[min_distant_vertex] = True

            # See all the connected vertices to min_distant_vertex one by one
            for connected_vertex in self.graph[min_distant_vertex]:
                con_vertex = connected_vertex[0]
                con_vertex_weight = connected_vertex[1]
                # If the connected_vertex is not in spt_set and also weight of connected_vertex + 
                # vertex_distance[min_distant_vertex] < vertex_distance[connected vertex],
                # then update the vertex_distance of connected_vertex and also 
                # it's parent to be the min_distant_vertex
                if(spt_set[con_vertex] == False and  
                    con_vertex_weight + vertex_distance[min_distant_vertex] < vertex_distance[con_vertex]):
                    vertex_distance[con_vertex] = con_vertex_weight + vertex_distance[min_distant_vertex]
                    parent[con_vertex] = min_distant_vertex
            
            # Again call the function to get new min_distant_vertex with updated spt_set and vertex_distance
            min_distant_vertex = self.get_min_distant_vertex_not_in_spt(spt_set, vertex_distance)
        

        # Print the edges and their respective weights using parent and vertex_distance dicts.
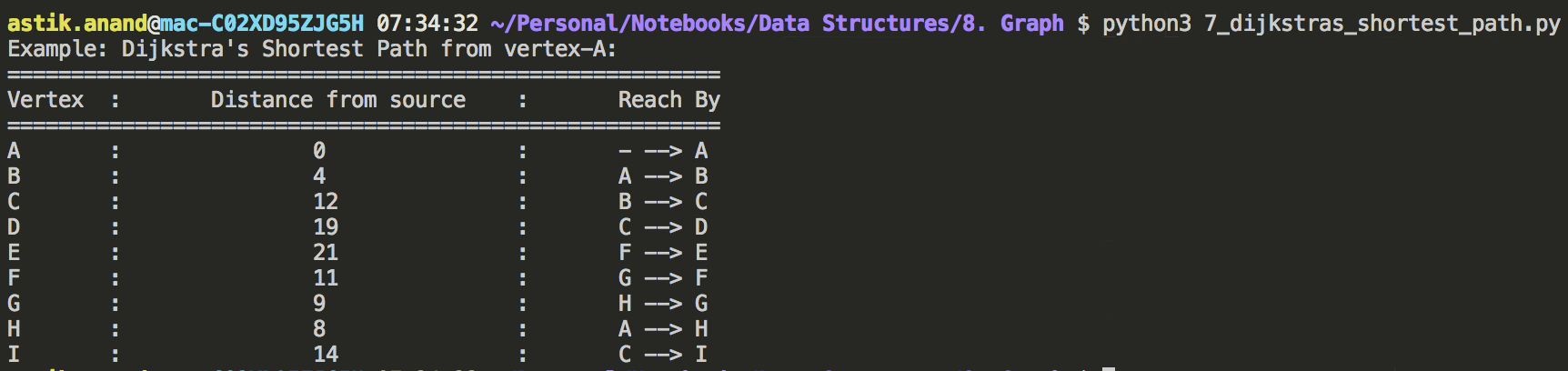
        ordered_parent = sorted(parent.items(), key=lambda k: (k[0]))
        print("="*56 + "\nVertex\t:\tDistance from source\t:\tReach By\n" + "="*56)
        for vertex, parent_vertex in ordered_parent:
            print("{}\t:\t\t{}\t\t:\t{} --> {}".format(vertex, vertex_distance[vertex], parent_vertex, vertex))
        


print("Example: Dijkstra's Shortest Path from vertex-A:")
g = Graph()
g.add_edge("A", "B", 4)
g.add_edge("A", "H", 8)
g.add_edge("B", "C", 8)
g.add_edge("B", "H", 11)
g.add_edge("C", "D", 7)
g.add_edge("C", "F", 4)
g.add_edge("C", "I", 2)
g.add_edge("D", "E", 9)
g.add_edge("D", "F", 14)
g.add_edge("E", "F", 10)
g.add_edge("F", "G", 2)
g.add_edge("G", "H", 1)
g.add_edge("G", "I", 6)
g.add_edge("H", "I", 7)
g.dijkstras_spt("A")

Output:

dijkstra_shortest_path_output

Complexity:
Notes:



6. Snake and Ladder Problem***

Problem:

Given a snake and ladder board, find the minimum number of dice throws required to reach the destination or last cell from source or 1st cell.Basically, the player has total control over outcome of dice throw and wants to find out minimum number of throws required to reach last cell.If the player reaches a cell which is base of a ladder, the player has to climb up that ladder and if reaches a cell is mouth of the snake, has to go down to the tail of snake without a dice throw.

Approach:
Implementation:
def get_min_dice_throws_snake_ladder(N, moves):
    # Mark every cell as unvisited and take an empty queue
    visited = [False]*(N)
    queue = []

    # Mark the first_cell as visited and enqueue the first cell to the queue 
    # with dice_count=0 : We start from here. 
    visited[0] = True
    queue.append((0, 0))

    while(queue):
        # Get the current element from the queue and then fetch the current_cell 
        # and current_dice_count from it.
        current = queue.pop(0)
        current_cell = current[0]
        current_dice_count = current[1]

        # if current_cell is last cell we are done, print the dice_count and break
        if(current_cell == N-1):
            print("No. of min dice count: {}".format(current_dice_count))
            break
        
        # Start seeing all the 6 reachable_cell from current_cell one by one
        for reachable_cell in range(current_cell+1, current_cell+6):
            # If reachable_cell is lesser than last cell and still not visited 
            # then mark the recahable_cell as visited
            if(reachable_cell < N and visited[reachable_cell] is False):
                visited[reachable_cell] = True
                # If any of ladder or snake is available at reachable_cell 
                # modify the reachable_cell with the moves value
                if(moves[reachable_cell] != -1):
                    reachable_cell = moves[reachable_cell]
                
                # Update the queue with reachable_cell and dice_count needed to reach there.
                queue.append((reachable_cell, current_dice_count+1))



print("Example-1:- Snake and Ladder:")
N = 30
moves = [-1] * N 
  
# Ladders 
moves[2] = 21
moves[4] = 7
moves[10] = 25
moves[19] = 28
  
# Snakes 
moves[26] = 0
moves[20] = 8
moves[16] = 3
moves[18] = 6
get_min_dice_throws_snake_ladder(N, moves)

Output:

snake_ladder-problem_output

Complexity:



7. Finding number of Islands

Problem:

Given a boolean 2D matrix, find the number of islands. A group of connected 1s forms an island.

Example:

Input :

matrix[][] : {1, 1, 0, 0, 0},

​ {0, 1, 0, 0, 1},

​ {1, 0, 0, 1, 1},

​ {0, 0, 0, 0, 0},

​ {1, 0, 1, 0, 1}

Output : 5 // Total 5 islands.

Connected Component

Important Facts:
Approach:
Implementation
POSSIBLE_MOVES = [(-1, -1), (-1, 0), (-1, 1), (0, -1), (0, 1), (1, -1), (1, 0), (1,1)]

class Graph:
    def __init__(self, matrix):
        self.graph = matrix
        self.row = len(matrix)
        self.col = len(matrix[0])
    

    def is_safe_cell(self, x, y, visited):
        # Cell is safe if x is in range(row), y is in range(column),
        # cell is still not visited and value of cell is 1.
        return (x>=0 and x<self.row and 
                y>=0 and y<self.col and 
                not visited[x][y] and self.graph[x][y] ==1)
    

    # Function to do DFS for a 2D boolean matrix, considers all the 8 neighbours as adjacent vertices.
    def DFS(self, i, j, visited):
        # Mark current_cell as visited
        visited[i][j] = True

        # For all neighbours check if the cell is safe then call the DFS again from that safe_cell.
        for x_move, y_move in POSSIBLE_MOVES:
            if(self.is_safe_cell(i+x_move, j+y_move, visited)):
                self.DFS(i+x_move, j+y_move, visited)


    def find_number_of_islands(self):
        # Mark all cells as unvisited initially
        visited = [[False]*self.col for i in range(self.row)]

        islands_count = 0
        for i in range(self.row):
            for j in range(self.col):
                # If a cell with value 1 is not visited yet, then new island is found
                # Visit all cells in this island and increment islands_count
                if(self.graph[i][j] == 1 and visited[i][j] is False):
                    self.DFS(i, j, visited)
                    islands_count += 1
        
        print("Total islands: {}".format(islands_count))



print("Example-1:- Find number of Islands:")
matrix=[[1, 1, 0, 0, 0], 
        [0, 1, 0, 0, 1], 
        [1, 0, 0, 1, 1], 
        [0, 0, 0, 0, 0], 
        [1, 0, 1, 0, 1]]
g = Graph(matrix)
g.find_number_of_islands()

Output:

number_of_islands_output

Complexity:





Problems To Do:



← Previous:  Hash






Subscribe !

Subscribe to the mailing list and get the latest updates in your mailbox.

Connect to me through Social Networks !

Get socially conneted on social networks and be updated.
LinkedIn GitHub StackOverflow Instagram

Contact Me !

You can reach me using below contact details.
  • Hyderabad, Telangana, India
  • +91-9037489697
  • +91-9037489697
  • astikanand@gmail.com