Segment Tree
What is Segment Tree ?
- Invented in 1977 by Jon Louis Bentley.
- Tree data structure used for storing information about intervals, or segments.
- In principle, it is a static structure that can’t be modified once it’s built.
- Useful in the areas of computational geometry, and geographic information systems.
Why Segment Tree ?
- Solves the problem of range queries in an array in O(Logn) time.
- Find min or max value in a certain range.
- Find sum of a certain range.
Understanding using Range Sum Query Problem***
Given an array array we need to find the sum of elements from index l to r where 0 <= l <= r <= n-1.
We should be able to change value of a specified element of the array to a new value x i.e. need to do arr[i] = x where 0 <= i <= n-1.
Approach-1: Simple
- A simple solution is to run a loop from l to r and calculate sum of elements in given range.
- To update a value, simply do arr[i] = x.
- Range Sum: O(n) time and Update: O(1) time.
- This works well if the number of query operations are very few and large updates.
Approach-2: Another Simple
- Create another array and store sum from start to i at the ith index in this array.
- Range Sum: O(1) time and Update: O(n) time.
- This works well if the number of query operations are large and very few updates.
Approach-3: Using Segment Tree
- We can use a Segment Tree to do both operations in O(Logn) time.
Segment Tree Representation
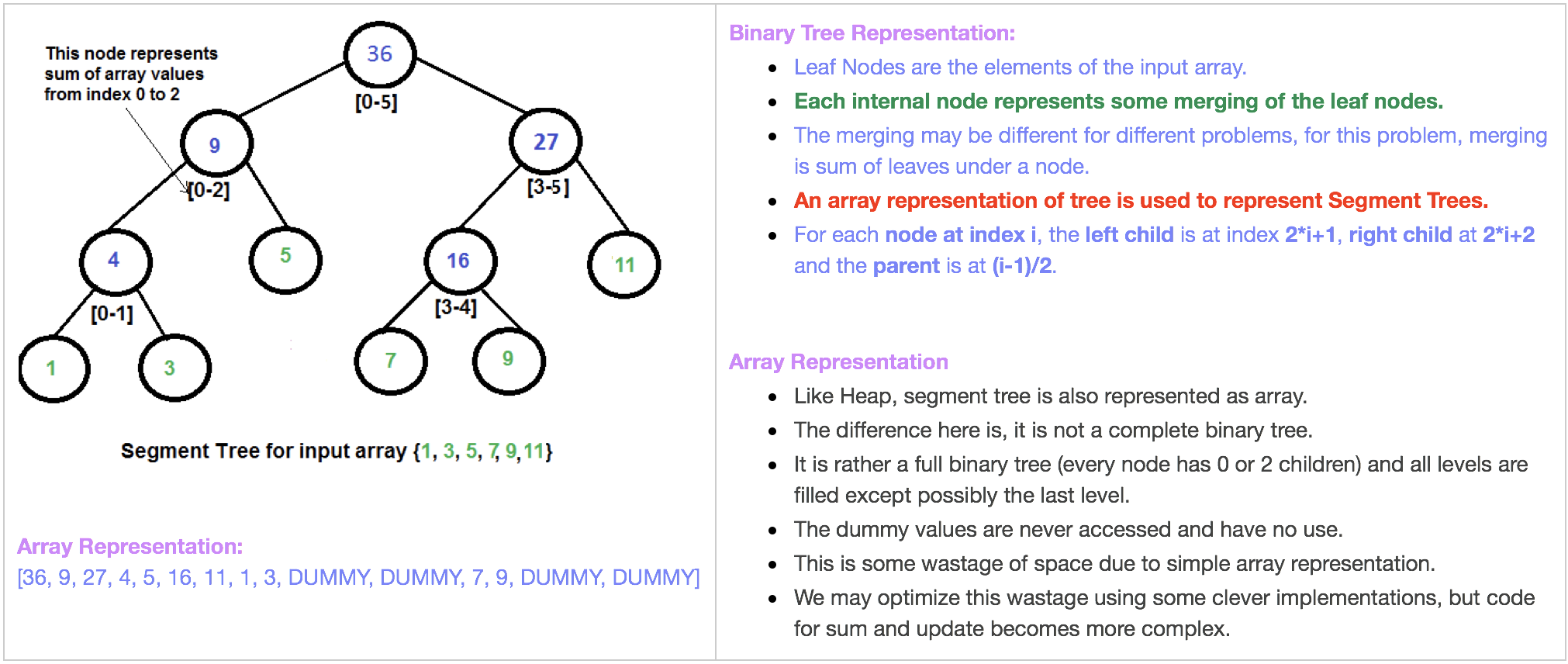
Segment Tree Construction
- As we know that each node of the segtree will represent an interval or segment.
- In this problem we need to find the sum of all the elements in the given range.
- So in each node we will store the sum of all the elements of the interval represented by the node.
- How do we do that? We will build a segment tree using recursion ( bottom-up approach ).
- Each leaf will have a single element. All the internal nodes will have the sum of both of its children.
- Complexity: O(N) as total node are appox 4N.
- Auxilliary Space: O(N) as total required are 3N extra.
Size of Array to Represent:
- If n is a power of 2:
- Then there will be no dummy nodes.
- So size of segment tree is 2n-1 (n leaf nodes and n-1) internal nodes.
- If n is not a power of 2:
- Then size of tree will be 2*x – 1 where x is smallest of power of 2 that is greater than n.
- Example, when n = 10, then size of array representing segment tree is 2*16-1 = 31.
- Coz here x=16 is smallest of power of 2 which is greater than 10.
Segment Tree Query
- To query on a given range, we need to check 3 conditions:
- Case-1: Range represented by the node [start, end] is completely outside the given_range [left, right.
- Case-2: Range represented by the node [start, end] is completely inside the given_range [left, right].
- Case-3: Range represented by a node [start, end] is partially inside and partially outside the given_range [left, right].
- Time Complexity: O(logN)
Segment Tree Update
- To update an element we need to look at the interval in which the element is and recurse accordingly on the left or the right child.
- Time Complexity: O(logN)
Implementation:
from math import pow, ceil, log
class SegmentTree:
def __init__(self, arr):
self.arr = arr
n = len(arr)
x = int(pow(2, ceil(log(n, 2))))
self.tree = ['-∞']*(2*x)
# We will build a segment tree using recursion (bottom-up approach).
# Each leaf will have a single element and all the internal nodes will have sum of both of its children.
# Complexity: O(N) as total node are appox 4N
# Auxilliary Space: O(N) as total required are 3N extra.
def build_tree(self, node, start, end):
if start == end:
self.tree[node] = self.arr[start]
else:
mid = (start + end) // 2
# Build for left child
self.build_tree(2*node, start, mid)
# Build for right child
self.build_tree(2*node+1, mid+1, end)
# Internal node will have the sum of both of its children
self.tree[node] = self.tree[2*node] + self.tree[2*node + 1]
# To query on a given range, we need to check 3 conditions, explained below with cases.
# node : [start, end] and given_range : [left, right]
# Complexity: O(logN)
def query(self, node, start, end, left, right):
# Case-1: Range represented by the node is completely outside the given range
if(right < start or end < left):
return 0
# Case-2: Range represented by the node is completely inside the given range
if(left <= start and end <= right):
return self.tree[node]
# Case-3: Range represented by a node is partially inside and partially outside the given range
mid = (start + end) // 2
val_1 = self.query(2*node, start, mid, left, right)
val_2 = self.query(2*node+1, mid+1, end, left, right)
return val_1 + val_2
# To update an element we need to look at the interval in which the element is and recurse
# accordingly on the left or the right child.
# Complexity: O(logN)
def update(self, node, start, end, index, val_diff):
if start == end:
self.tree[node] += val_diff
else:
mid = (start + end) // 2
if start <= index and index <= mid:
self.update(2*node, start, mid, index, val_diff)
else:
self.update(2*node+1, mid+1, end, index, val_diff)
# Internal node will have the sum of both of its children
self.tree[node] = self.tree[2*node] + self.tree[2*node+1]
# Driver Program
seg_tree = SegmentTree([1, 3, 5, 7, 9, 11])
seg_tree.build_tree(1, 0, 5)
print("Newly Built Segment Tree:")
print(seg_tree.tree)
print("Sum in Range [1, 3] : {}".format(seg_tree.query(1, 0, 5, 1, 3 )))
print("\nUpdating index 1 from 3 to 10: increment by 7.")
seg_tree.update(1, 0, 5, 1, 7)
print("Segment Tree after Update:")
print(seg_tree.tree)
print("Sum in Range [1, 3] after update: {}".format(seg_tree.query(1, 0, 5, 1, 3 )))
Output:

Complexity:
- Time: Build - O(N), Query: O(logN), Update: O(logN)
- Auxilliary Space: O(N) for build
Lazy Segment Tree***
Sometimes problems ask us to update an interval from l to r, instead of a single element.
Approach-1: Update one by one
- To update a single element it takes O(logn) time and in worst case we need to update n elements.
- Time Complexity: O(nlogn)
Approach-2: Introducing Laziness : Do work only when needed
- When we need to update an interval, we will update a node and mark its child that it needs to be updated and update it when needed.
- For this we need an array lazy[] of the same size as that of segment tree.
- Initially all the elements of the lazy[] array will be 0 representing that there is no pending update.
- If there is non-zero element lazy[k] then this element needs to update node k in the segment tree before making any query operation.
Modify Update Function with Laziness
- To update an interval lazily we need to handle 4 different cases:
- Case-1: If the interval represented by current node has pending updates, then update the current node, mark children as lazy and reset the current lazy node.
- Case-2: If the interval represented by current node lies completely outside the given interval to update, then ignore it.
- Case-3: If the interval represented by current node lies completely in the given interval to update, then update the current node and mark children as lazy.
- Case-4: If the interval represented by current node overlaps with the given interval to update, then update the both children recursively and finally update the current node.
- Time Complexity: O(logn)
- Auxilliary Space: O(N) for lazy array
Modify Query Function coz of Laziness
- Since we have changed the update function to postpone the update operation, we will have to change the query function also.
- To query for an interval, we need to handle 4 different cases:
- Case-1: If the interval represented by current node has pending updates, then update the current node, mark children as lazy and reset the current lazy node.
- Case-2: If the interval represented by current node lies completely outside the given interval to query, then return 0.
- Case-3: If the interval represented by current node lies completely inside the given interval to query, then simply return the current node value.
- Case-4: If the interval represented by current node overlaps with the given interval to query, query the left and right child and return the total of both.
- Time Complexity: O(logn)
Implementation:
from math import pow, ceil, log
class LazySegmentTree:
def __init__(self, arr):
self.arr = arr
n = len(arr)
x = int(pow(2, ceil(log(n, 2))))
self.tree = ['-∞']*(2*x)
self.lazy = [0]*(2*x)
def build_tree(self, node, start, end):
if start == end:
self.tree[node] = self.arr[start]
else:
mid = (start + end) // 2
# Build for left child
self.build_tree(2*node, start, mid)
# Build for right child
self.build_tree(2*node+1, mid+1, end)
# Internal node will have the sum of both of its children
self.tree[node] = self.tree[2*node] + self.tree[2*node + 1]
def lazy_update(self, node, start, end, left, right, val):
# Case-1: If the interval represented by current node has pending updates,
# then update the current node, mark children as lazy and reset the current lazy node.
if self.lazy[node] != 0:
self.tree[node] += (end-start+1)*self.lazy[node]
if start != end:
self.lazy[2*node] += self.lazy[node] # Mark left child lazy
self.lazy[2*node+1] += self.lazy[node] # Mark right child lazy
# Reset the lazy node
self.lazy[node] = [0]
# Case-2: If the interval represented by current node lies completely outside the given interval
# to update, then ignore it.
if (start > end or right < start or end < left):
return
# Case-3: If the interval represented by current node lies completely in the given interval to update,
# then update the current node and mark children as lazy.
if (left <= start and end <= right):
self.tree[node] += (end-start+1)*val
if start != end:
# Mark children as lazy
self.lazy[2*node] += val # Mark left child lazy
self.lazy[2*node+1] += val # Mark right child lazy
return
# Case-4: If the interval represented by current node overlaps with the given interval to update,
# then update the both children recursively and finally update the current node.
mid = (start + end) // 2
self.lazy_update(2*node, start, mid, left, right, val) # Updating left child
self.lazy_update(2*node+1, mid+1, end, left, right, val) # Updating right child
self.tree[node] = self.tree[2*node] + self.tree[2*node+1] # Updating using children
def lazy_query(self, node, start, end, left, right):
# Case-1: If the interval represented by current node has pending updates,
# then update the current node, mark children as lazy and reset the current lazy node.
if self.lazy[node] != 0:
self.tree[node] += (end-start+1)*self.lazy[node]
if start != end:
self.lazy[2*node] += self.lazy[node] # Mark left child lazy
self.lazy[2*node+1] += self.lazy[node] # Mark right child lazy
# Reset the lazy node
self.lazy[node] = [0]
# Case-2: If the interval represented by current node lies completely outside the given interval
# to query, then return 0.
if (start > end or right < start or end < left):
return 0
# Case-3: If the interval represented by current node lies completely inside the given interval
# to query, then simply return the current node value.
if (left <= start and end <= right):
return self.tree[node]
# Case-4: If the interval represented by current node overlaps with the given interval to query,
# query the left and right child and return the total of both.
mid = (start + end) // 2
val_1 = self.lazy_query(2*node, start, mid, left, right); # Query left child
val_2 = self.lazy_query(2*node+1, mid+1, end, left, right); # Query right child
return val_1 + val_2
# Driver Program
lazy_seg_tree = LazySegmentTree([1, 3, 5, 7, 9, 11])
lazy_seg_tree.build_tree(1, 0, 5)
print("Newly Built Lazy Segment Tree:")
print("Tree: {}".format(lazy_seg_tree.tree))
print("Lazy Arr: {}".format(lazy_seg_tree.lazy))
print("Sum in Range [1, 3] : {}".format(lazy_seg_tree.lazy_query(1, 0, 5, 1, 3 )))
print("\nUpdate by adding 10 to all nodes at indexes from 1 to 5")
lazy_seg_tree.lazy_update(1, 0, 5, 1, 5, 10)
print("Lazy Segment Tree after Update:")
print("Tree: {}".format(lazy_seg_tree.tree))
print("Lazy Arr: {}".format(lazy_seg_tree.lazy))
print("Sum in Range [1, 3] after update: {}".format(lazy_seg_tree.lazy_query(1, 0, 5, 1, 3 )))
Output:

Complexity:
- Time: Build - O(N), Query: O(logN), Update: O(logN)
- Auxilliary Space: O(N) for build, query and update