Dynamic Programming Approach
What is Dynamic Programming Approach ?
-
It is an algorithmic paradigm that solves a given complex problem by breaking it into subproblems and storing the results of subproblems to avoid computing the same results again.
- Utilizes the fact that the optimal solution to the overall problem depends on the optimal solutions to its subproblems.
- Example: Fibonacci numbers - We can calculate nth Fibonacci by below eqution
fib(n) = fib(n-1) + fib(n-2) for n > 1
- Here to solve the overall problem we broke it down to smaller subproblems.
Characteristics of Dynamic Programming
- Subproblems are smaller version of the original problem.
- Any problem has overlappping subproblems if finding its solution involves solving the same subproblem multiple times.
- Like Divide and Conquer, Dynamic Programming combines solutions to sub-problems.
- Dynamic Programming is mainly used when solutions of same subproblems are needed again and again.
- In dynamic programming, computed solutions to subproblems are stored in a table so that these don’t have to be recomputed.
- Dynamic Programming is not useful when there are no common (overlapping) subproblems because there is no point storing the solutions if they are not needed again.
- Binary Search is broken down into subproblems but it doesn’t have common subproblems, so no sense to store the solutions.
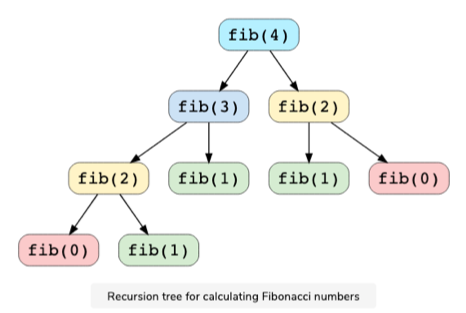
- Here we can see overlapping subproblems as fib(2) is evaluated twice and fib(1) evaluated thrice.
2. Optimal Substructure Property
-
Any problem has optimal substructure property if its overall optimal solution can be constructed from optimal solution of subproblems.
-
fib(n)= fib(n-1)+fib(n-2)- shows that overall problem of size n is reduced to subproblems of size n-1 and n-2. -
Example:- The Shortest Path problem has following optimal substructure property:
- If a node x lies in the shortest path from a source node u to destination node v.
- Then the shortest path from u to v is combination of shortest path from u to x and shortest path from x to v.
- The standard All Pair Shortest Path algorithms like Floyd–Warshall and Bellman–Ford are typical examples of Dynamic Programming.
-
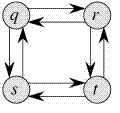
But the Longest Path problem i.e. longest simple path (path without cycle) between two nodes doesn’t have the Optimal Substructure property.
- There are two longest paths from q to t: q→r→t and q→s→t.
- Unlike shortest paths, these longest paths do not have the optimal substructure property.
- Example:- The longest path q→r→t is not a combination of longest path from q to r and longest path from r to t.
- Coz the longest path from q to r is q→s→t→r and the longest path from r to t is r→q→s→t.
Methods to Solve Dynamic Programming Problem
1. Recursion + Memoization (Top-Down Approach)
- Solve bigger problem by recursiverly finding the solution to smaller sub-problems.
- Whenever we solve a sub-problem we cache its result to avoid calling it multiple times.
- This technique of storing the results of already solved subproblems k/a Memoization.
2. Iteration + Tabulation (Bottom-Up Approach)
- Tabulation is opposite of Top-Down Approach and avoids recursion.
- In this we solve the problem bottom up (i.e by solving all the related subproblems first).
- This is typically done by filling an n-dimensional table.
- Based on the results in the table, the solution to the top/orignal problem is computed.
- Both Tabulated and Memoized store the solutions of subproblems.
- In Memoized version, table is filled on demand but in Tabulated version, starting from the first entry, all entries are filled one by one.
- Unlike the Tabulated version, all entries of the lookup table are not necessarily filled in Memoized version.
- Example:- Memoized solutionof the LCS problem doesn’t necessarily fill all entries.
Standard Dynamic Programming Problems
1. Maximum Sum Subarray***
Problem:
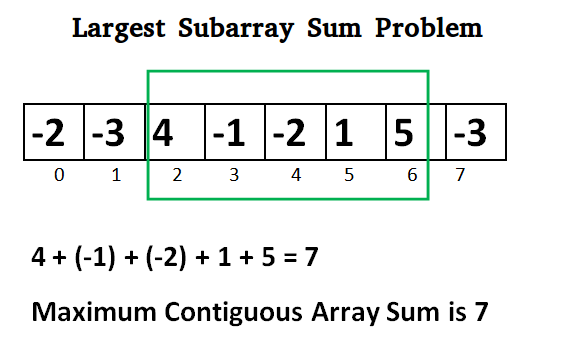
Find the sum of contiguous subarray within a one-dimensional array of numbers which has the largest sum.
Kadane’s Algorithm:
- Use Kadane’s DP approach.
Implementation
def maxSubArray(nums):
current_sum = max_sum = float("-inf")
start = end = s = 0
for i, num in enumerate(nums):
if (current_sum < 0):
current_sum = num
s = i
else:
current_sum += num
if(current_sum >= max_sum):
max_sum = current_sum
end = i
start = s
print(f"Max : {max_sum} and Subarray : {nums[start:end + 1]}")
maxSubArray([-2, -3, 4, -1, -2, 1, 5, -3])
maxSubArray([-2, 1, -3, 4, -1, 2, 1, -5, 4])
maxSubArray([1])
maxSubArray([0])
maxSubArray([-1])
maxSubArray([-5, -3, -2, -4])
Output:
Max : 7 and Subarray : [4, -1, -2, 1, 5]
Max : 6 and Subarray : [4, -1, 2, 1]
Max : 1 and Subarray : [1]
Max : 0 and Subarray : [0]
Max : -1 and Subarray : [-1]
Max : -2 and Subarray : [-2]
Complexity:
- Time: O(n) :- Loop runs till n
- Auxilliary Space: O(1)
2. Subset Sum Problem***
Problem:
Given a set of non-negative integers, and a value sum, determine if there is a subset of the given set with sum equal to given sum.
Example:
Input: set[] = {3, 34, 4, 12, 5, 2}, sum = 11
Output: True //There is a subset (4, 5, 2) with sum 11.
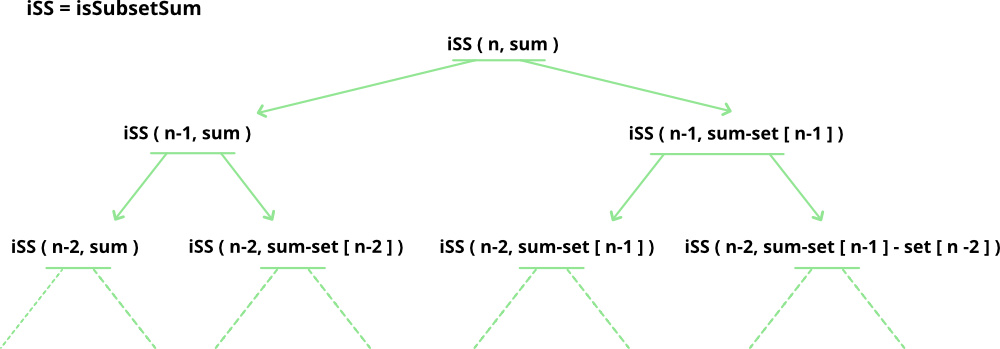
Recursive Approach:
-
is_subset_sum(set, n, sum) = is_subset_sum(set, n-1, sum) is_subset_sum(set, n-1, sum-set[n-1]) - Base Cases:
- is_subset_sum(set, n, sum) = false, if sum > 0 and n == 0
- is_subset_sum(set, n, sum) = true, if sum == 0
Recursive Implementation:
def is_subset_sum_recursive(given_set, n, given_sum):
if(given_sum==0):
return True
if(n==0 and given_sum != 0):
return False
return is_subset_sum_recursive(given_set, n-1, given_sum) or
is_subset_sum_recursive(given_set, n-1, given_sum-given_set[n-1])
print("Example-1: is_subset_sum_recursive(given_set, n, given_sum)")
given_set = [1, 3, 9, 2]
print(is_subset_sum_recursive(given_set, 4, 5))
print("Example-2: is_subset_sum_recursive(given_set, n, given_sum)")
given_set = [3, 34, 4, 12, 5, 2]
print(is_subset_sum_recursive(given_set, 6, 11))
print("Example-3: is_subset_sum_recursive(given_set, n, given_sum)")
given_set = [3, 34, 4, 12, 5, 2]
print(is_subset_sum_recursive(given_set, 6, 13))
Output

Complexity:
- Time: O(2n) :- Every number will either be picked or not hence 222……. = 2n.
- Auxilliary Space: O(n)
Notes:
- The above solution may try all subsets of given set in worst case.
- Therefore time complexity of the above solution is exponential.
- The problem is in-fact NP-Complete (There is no known polynomial time solution for this problem).
Dynamic Programming Approach:
- We can solve the problem in Pseudo-polynomial time using Dynamic programming.
- Create a boolean 2D table[][] and fill it in bottom up manner.
- The value of
table[i][j]will be true if there is a subset of set[0..j-1] with sum equal to i., otherwise false. - Finally, return table
[sum][n].
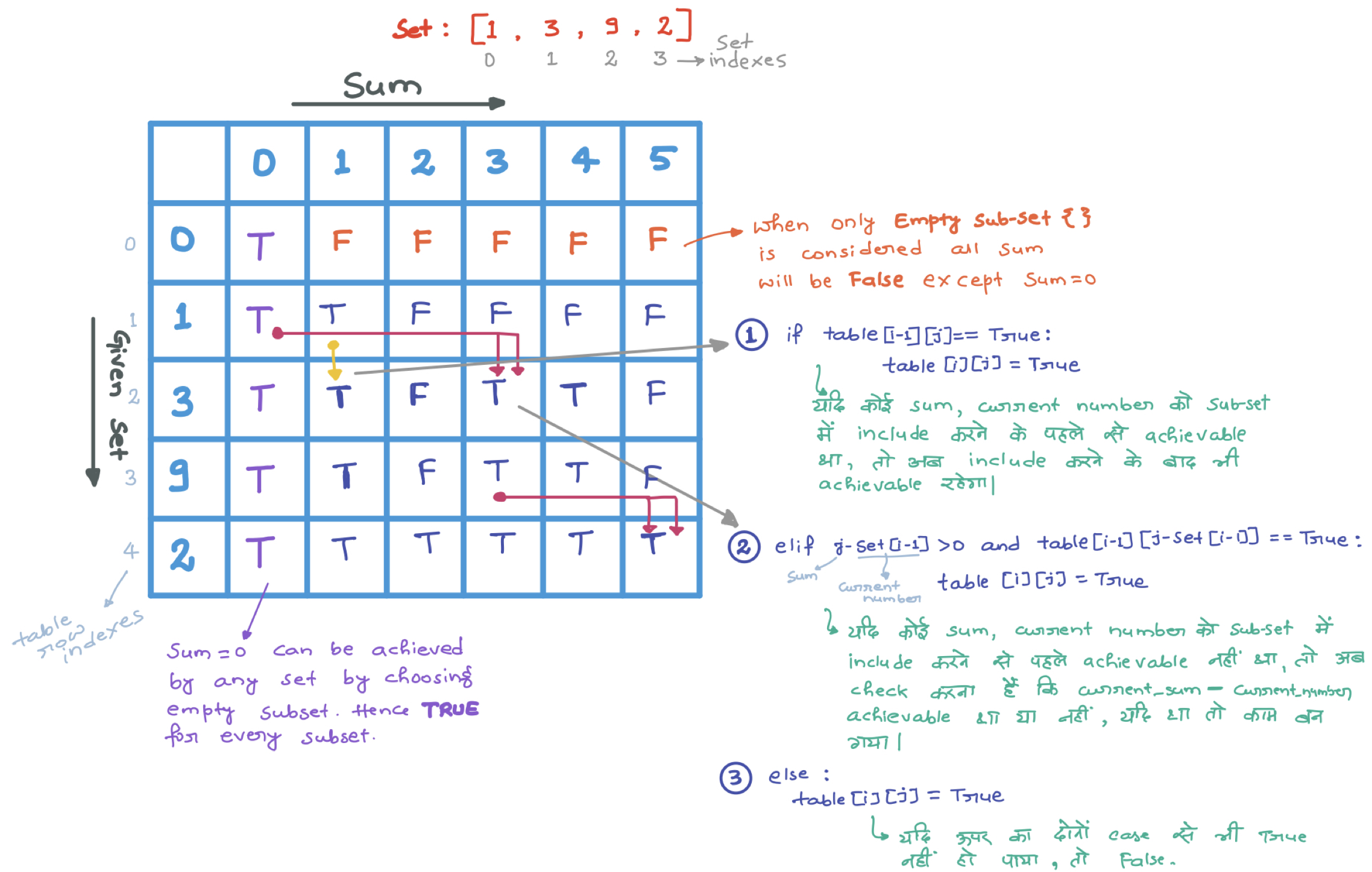
Dynamic Programming Implementation:
def is_subset_sum_dp(given_set, n, given_sum):
table = [[False]*(given_sum+1) for i in range(n+1)]
# Sum = 0 can be achieved by any subset by taking an empty set
for i in range(n+1):
table[i][0] = True
# With empty set all the sum will be False except sum=0
for i in range(1, given_sum+1):
table[0][i] = False
# Now fill the rest of table
for i in range(1, n+1):
for j in range(1, given_sum+1):
# If earlier (before adding this number in set) sum was possible,
# the now also it will be possible
if(table[i-1][j] == True):
table[i][j] = True
# If earlier not possible check if current_sum-current_number was possible earlier,
# if it was then we are done.
elif(j-given_set[i-1]>=0 and table[i-1][j-given_set[i-1]] == True):
table[i][j] = True
# If above 2 cases is not there, then False
else:
table[i][j] = False
return table[n][given_sum]
print("Example-1: is_subset_sum_dp(given_set, n, given_sum)")
given_set = [1, 3, 9, 2]
print(is_subset_sum_dp(given_set, 4, 5))
print("Example-2: is_subset_sum_dp(given_set, n, given_sum)")
given_set = [3, 34, 4, 12, 5, 2]
print(is_subset_sum_dp(given_set, 6, 11))
print("Example-3: is_subset_sum_dp(given_set, n, given_sum)")
given_set = [3, 34, 4, 12, 5, 2]
print(is_subset_sum_dp(given_set, 6, 13))
Output:

Complexity:
- Time: O(sum) :- Loop till max_num in set
- Auxilliary Space: O(n*sum)
3. Minimum Jumps to Reach End***
Problem:
Given an array of integers where each element represents the max number of steps that can be made forward from that element.
Write a function to return the minimum number of jumps to reach the end of the array (starting from the first element).
If an element is 0, then cannot move through that element.
Example:
Input: arr[] = {2, 3, 1, 2, 3, 4, 2, 0, 8, 1}
Output: 4 (2-> 3-> 2-> 4-> 1)
Recursive Approach:
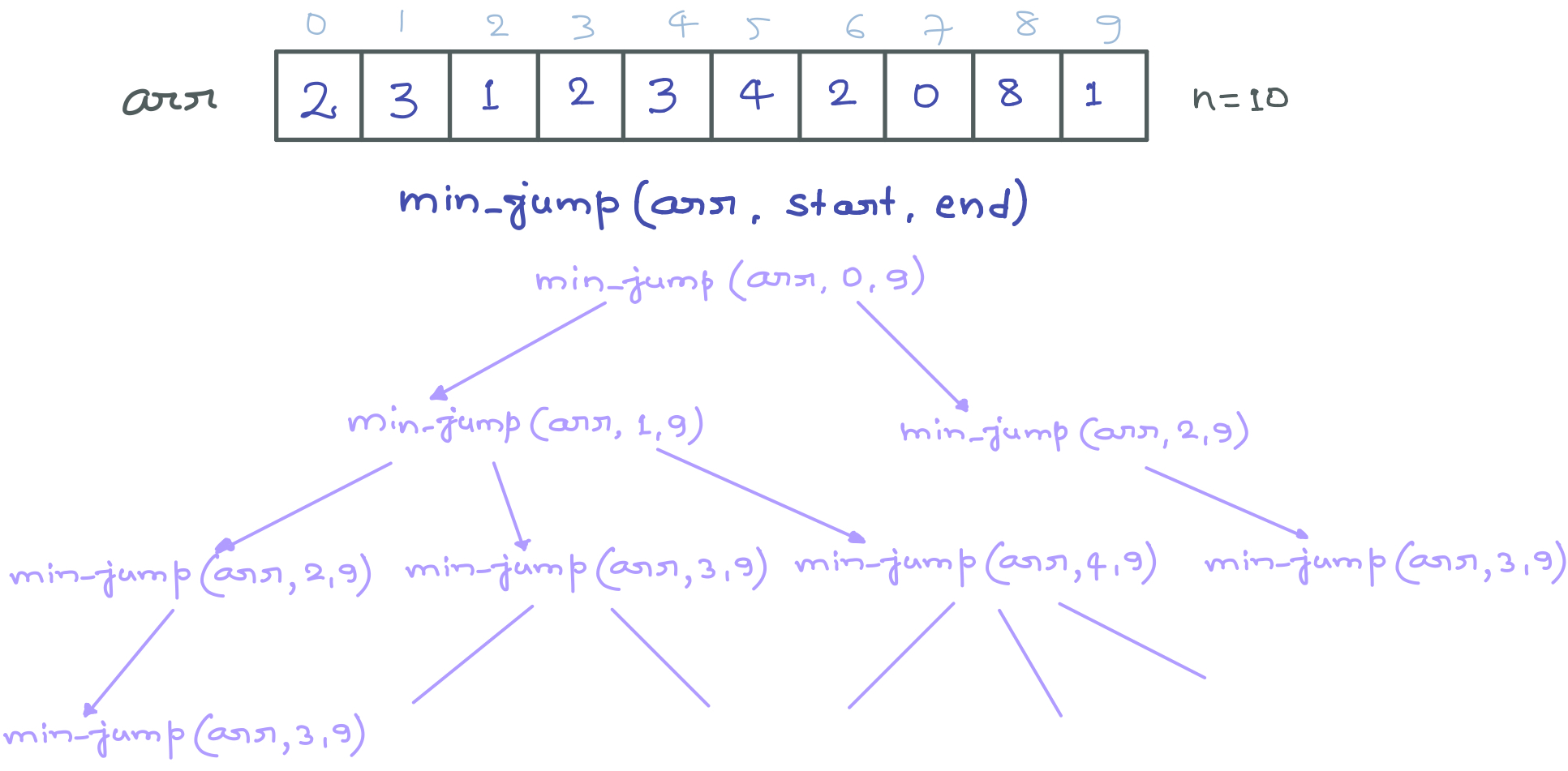
Recursive Implementation:
import sys
def min_jump_to_reach_end_recursive(arr, start, end):
# Base case: when start position and end position are same
if (start == end):
return 0
# When nothing is reachable from the given position
if (arr[start] == 0):
return sys.maxsize
# Just check where you can reach from start and then call min_jump from there
min_jumps = sys.maxsize
for i in range(1, arr[start]+1):
next_start = start+i
if(next_start < n):
jumps = 1 + min_jump_to_reach_end_recursive(arr, next_start, end)
if (jumps < min_jumps):
min_jumps = jumps
return min_jumps
print("Min Jump Recursive Example-1: min_jump_to_reach_end_recursive(arr, start, end)")
arr = [2, 3, 1, 2, 3, 4, 2, 0, 8, 1]
n = len(arr)
jumps = min_jump_to_reach_end_recursive(arr, 0, n-1)
if(jumps == sys.maxsize):
print("Unreachable")
else:
print("Jumps: {}".format(jumps))
print("\nMin Jump Recursive Example-2: min_jump_to_reach_end_recursive(arr, start, end)")
arr = [2, 3, 1, 2, 3, 2, 1, 0, 8, 1]
n = len(arr)
jumps = min_jump_to_reach_end_recursive(arr, 0, n-1)
if(jumps == sys.maxsize):
print("Unreachable")
else:
print("Jumps: {}".format(jumps))
Output:

Complexity:
- Time: O(2n) :- Every number will either be picked or not hence 222……. = 2n.
- Auxilliary Space: O(n)
Dynamic Programming Approach:
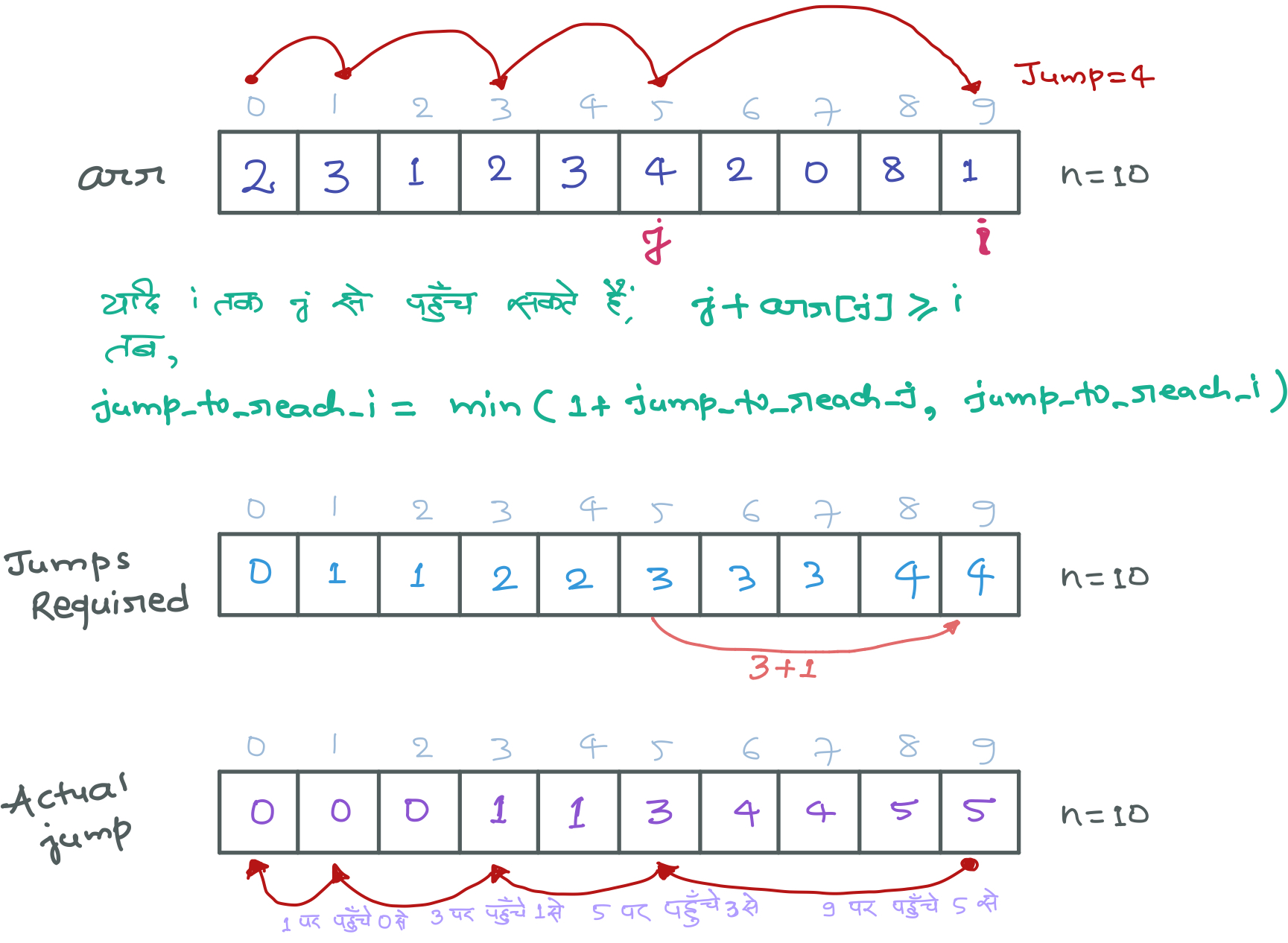
Dynamic Programming Implementation:
def min_jump_to_reach_end_DP(arr):
n = len(arr)
# Initialize jumps_required as "infinity" for every element
jumps_required = [sys.maxsize]*n
actual_jump = [0]*n
# First element is reachable by 0 jumps
jumps_required[0] = 0
for i in range(1, n):
for j in range(i):
# Check if from j we can reach i or not??
# If j + arr[j] >= i : then we can reach i
if(j+arr[j] >= i):
# If i is reachable from j in lesser jumps than earlier update the jumps to reach i
# Update the actual jump table also
if(jumps_required[j]+1 < jumps_required[i]):
jumps_required[i] = jumps_required[j]+1
actual_jump[i] = j
# Now print number of jumps and actual jump
if(jumps_required[n-1] == sys.maxsize):
print("Unreachable")
else:
print("Jumps: {}".format(jumps_required[n-1]))
k = n-1
print("Actual Jumps: end", end="")
while(k>0):
print("<--{}".format(actual_jump[k]), end="")
k = actual_jump[k]
print()
print("Min Jump DP Example-1: min_jump_to_reach_end_DP(arr)")
arr = [2, 3, 1, 2, 3, 4, 2, 0, 8, 1]
min_jump_to_reach_end_DP(arr)
print("\nMin Jump DP Example-2: min_jump_to_reach_end_DP(arr)")
arr = [2, 3, 1, 2, 3, 2, 1, 0, 8, 1]
min_jump_to_reach_end_DP(arr)
Output:

Complexity:
- Time: O(n2) :- 2 for loops
- Auxilliary Space: O(n)
Note:
There exists a O(n) solution to be discussed later.
4. Coin Change - Unique Ways***
Problem:
Given a value N, if we want to make change for N cents, and we have infinite supply of each of S = { S1, S2, .. , Sm} valued coins.
How many unique ways can we make the change? The order of coins doesn’t matter.
Example:
Input: N = 5 and S = {1, 2, 5} Output: 4 {1,1,1,1,1}, {1,1,1,2}, {1,2,2}, {5}.
Input: N = 10 and S = {2, 5, 3, 6} Output: 5 {2,2,2,2,2}, {2,2,3,3}, {2,2,6}, {2,3,5} and {5,5}
Recursive Approach:
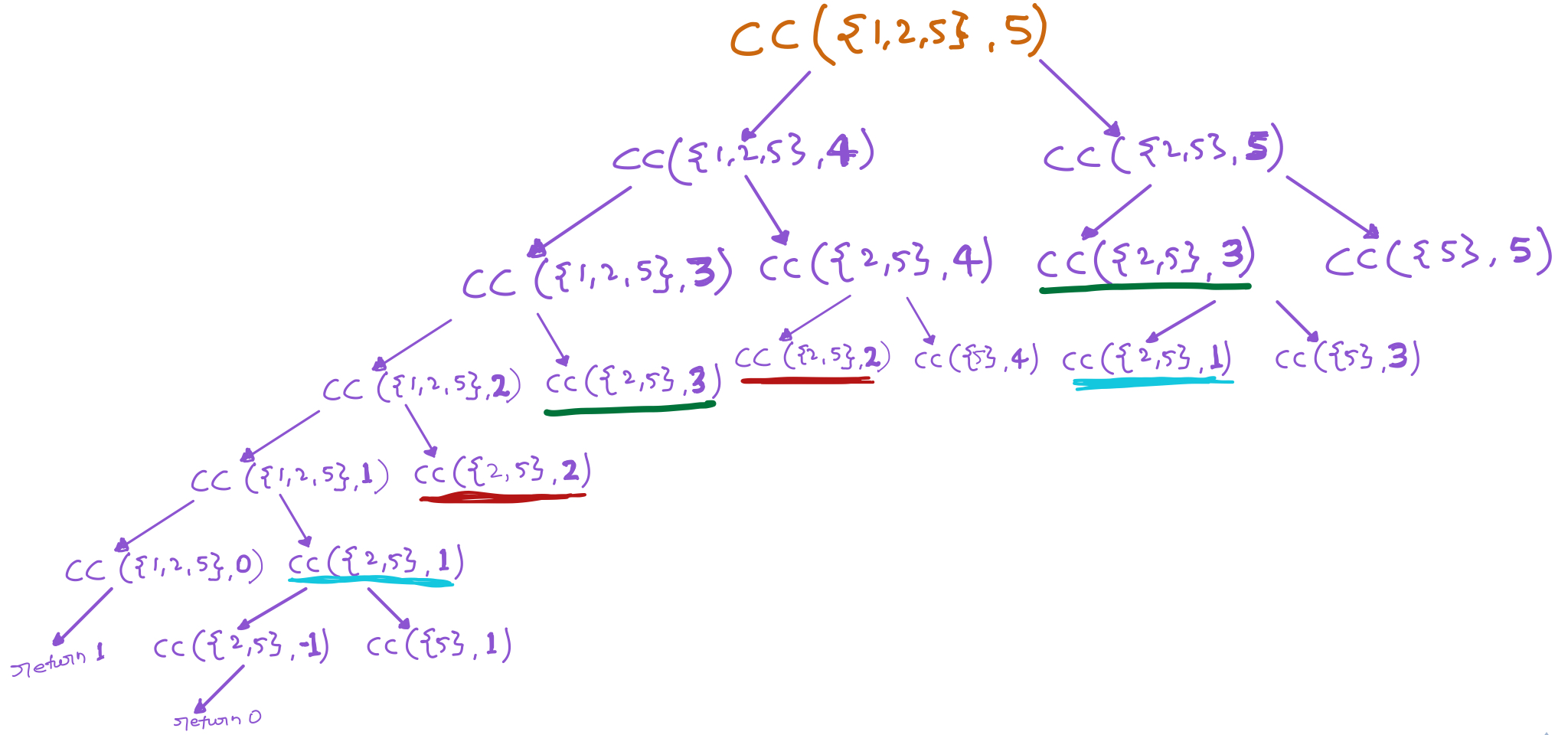
Recursive Implementation:
def coin_change_unique_ways_recursive(coins, N):
m = len(coins)
# If N is less than 0 then no solution exists
if (N < 0):
return 0
# If N is 0 then 1 solution : Don't include any coin
if (N == 0):
return 1
# If no coins, no solution exist
if (m == 0):
return 0
# Answer is sum of solutions (i)including first coin (ii) excluding first coin
return coin_change_unique_ways_recursive(coins, N-coins[0]) +
coin_change_unique_ways_recursive(coins[1:], N)
print("Example-1: coin_change_unique_ways_recursive(coins, N)")
coins = [1, 2, 5]
print(coin_change_unique_ways_recursive(coins, 5))
print("Example-2: coin_change_unique_ways_recursive(coins, N)")
coins = [2, 5, 3, 6]
print(coin_change_unique_ways_recursive(coins, 10))
Output:

Complexity:
- Time: O(2n) :- Every coin will either be picked or not hence 222……. = 2n.
- Auxilliary Space: O(n)
Dynamic Programming Approach:
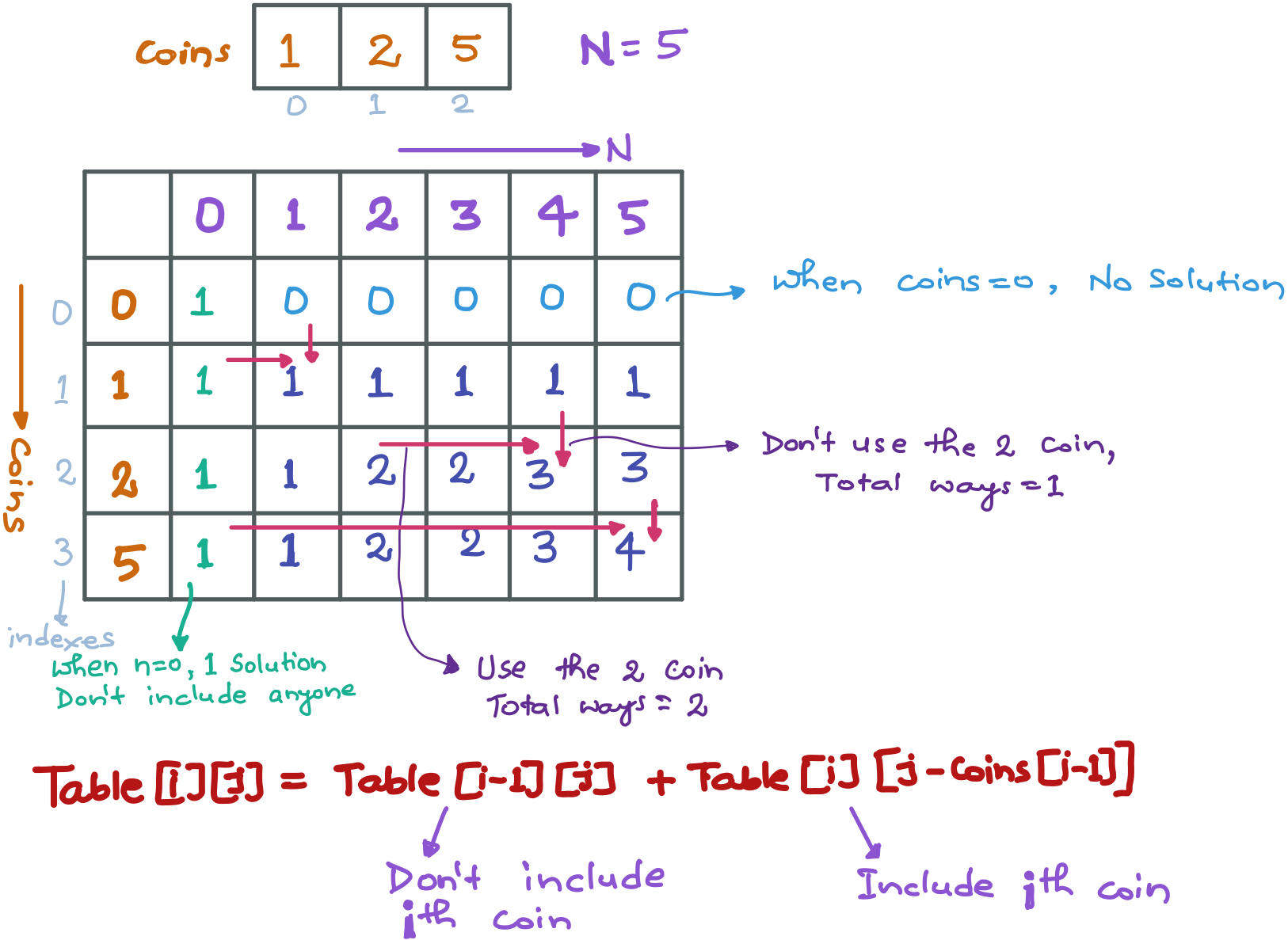
Dynamic Programming Implementation:
def coin_change_unique_ways_DP(coins, N):
m = len(coins)
table = [[0]*(N+1) for i in range(m+1)]
# when N=0, 1 solution:- Don't include anyone --- Fill first column
for i in range(m+1):
table[i][0] = 1
# When No coins or m = 0 :- No solution possible ---- Fill first row
# Line can be omitted as table is initialized with 0, just for better understanding
for j in range(1, N+1):
table[0][j] = 0
# Fill rest of the table
# table[i][j] = table[i-1][j] + table[i][j-coins[i-1]]
# table[i][j] = (Not including current coin) + (Including current coin)
for i in range(1, m+1):
for j in range(1, N+1):
# Can't include current coin
if(j-coins[i-1] < 0):
table[i][j] = table[i-1][j]
else:
table[i][j] = table[i-1][j] + table[i][j-coins[i-1]] # Include current coin
return table[m][N]
print("Example-1: coin_change_unique_ways_DP(coins, N)")
coins = [1, 2, 5]
print(coin_change_unique_ways_DP(coins, 5))
print("Example-2: coin_change_unique_ways_DP(coins, N)")
coins = [2, 5, 3, 6]
print(coin_change_unique_ways_DP(coins, 10))
Output:

Complexity:
- Time: O(mn) :- 2 for loops
- Auxilliary Space: O(mn)
5. Coin Change - Min Coins***
Problem:
Given a value V, if we want to make change for V cents, and we have infinite supply of each of C = { C1, C2, .. , Cm} valued coins.
What is the minimum number of coins to make the change?
Example:
Input: N = 11 and S = {1, 5, 6, 8} Output: 2 {5, 6}
Recursive Approach:
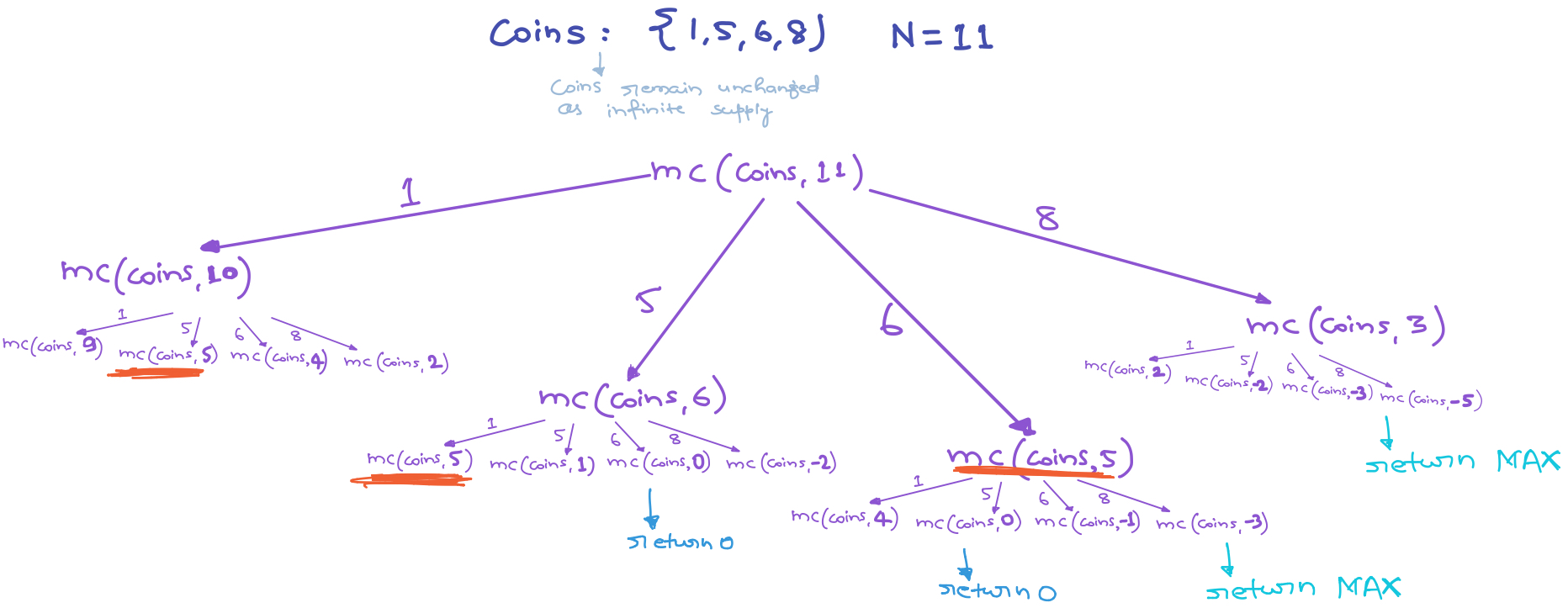
Implementation
import sys
def coin_change_min_coins_recursive(coins, N):
m = len(coins)
# if N==0, No coins needed
if(N == 0):
return 0
# if N < 0, return MAX and also when no coins
if(N < 0 or m == 0):
return sys.maxsize
# Now find minimum no. of coins by including every coin one by one
min_coins = sys.maxsize
for i in range(m):
min_coins = min(1 + coin_change_min_coins_recursive(coins, N-coins[i]), min_coins)
return min_coins
print("Example-1: coin_change_min_coins_recursive(coins, N)")
coins = [1, 5, 6, 8]
print(coin_change_min_coins_recursive(coins, 11))
print("Example-2: coin_change_min_coins_recursive(coins, N)")
coins = [2, 5, 7]
print(coin_change_min_coins_recursive(coins, 3))
Output:

Complexity:
- Time: Exponential
- Auxilliary Space: O(n)
Dynamic Programming Approach:
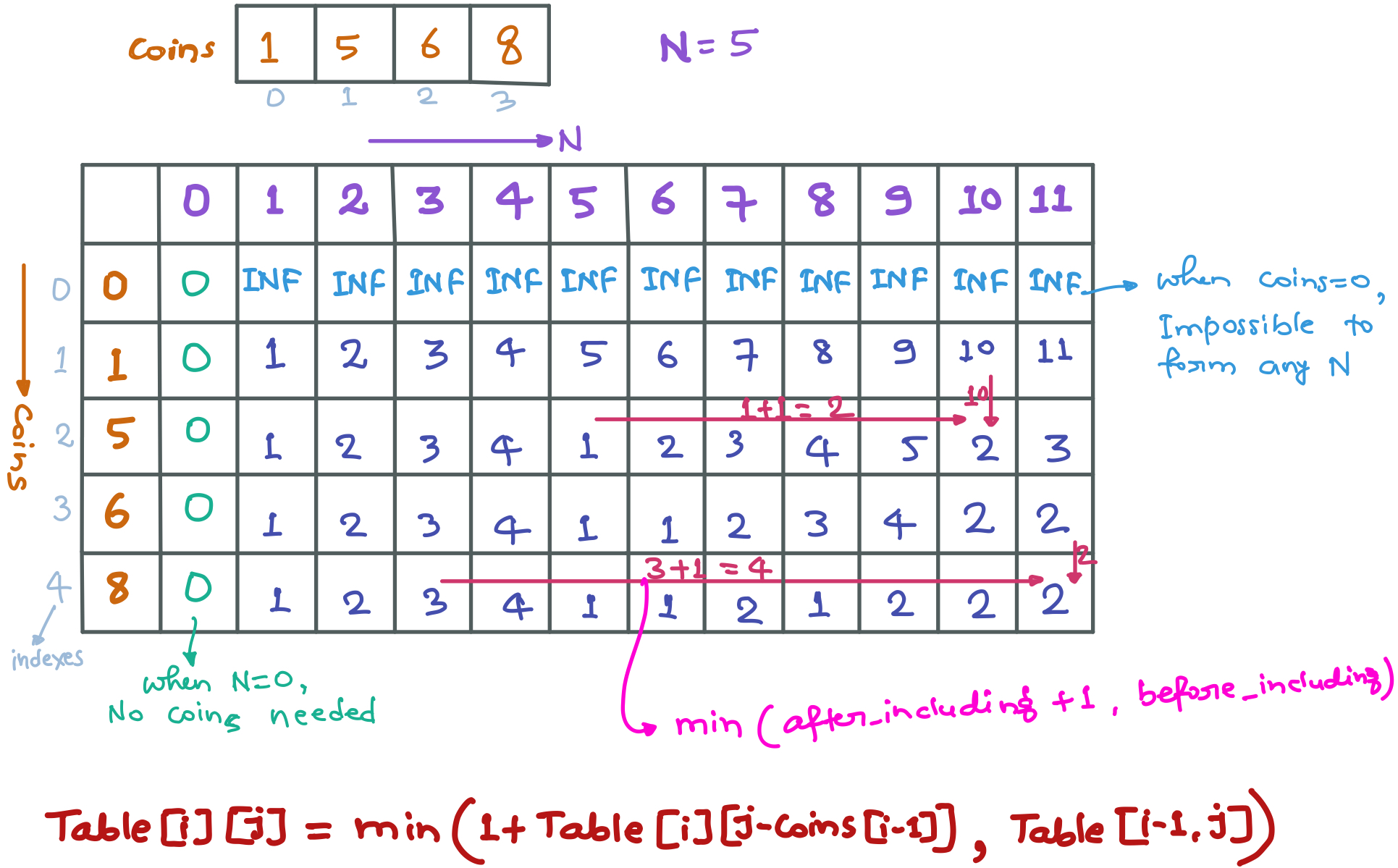
Dynamic Programming Implementation:
def coin_change_min_coins_DP(coins, N):
m = len(coins)
table = [[sys.maxsize]*(N+1) for i in range(m+1)]
# If N = 0 then coins required = 0 --- Fill first column
for i in range(m+1):
table[i][0] = 0
# If coins = 0 then coins required = INFINITY --- Fill first column
# This line can be omitted, just for understanding as we have initialized with infinity
for j in range(1, N+1):
table[0][j] = sys.maxsize
# Now fill the table
for i in range(1, m+1):
for j in range(1, N+1):
if(j-coins[i-1] < 0):
table[i][j] = table[i-1][j]
else:
table[i][j] = min(1+table[i][j-coins[i-1]], table[i-1][j])
return table[m][N]
print("Example-1: coin_change_min_coins_DP(coins, N)")
coins = [1, 5, 6, 8]
print(coin_change_min_coins_DP(coins, 11))
print("Example-2: coin_change_min_coins_DP(coins, N)")
coins = [2, 5, 7]
print(coin_change_min_coins_DP(coins, 3))
Output:

Complexity:
- Time: O(mn) :- 2 for loops
- Auxilliary Space: O(mn)
6. Ways to reach nth stair
Problem:
There are n stairs, a person standing at the bottom wants to reach the top. The person can climb either 1 stair or 2 stairs at a time.
Count the number of ways, the person can reach the top.
Examples:
Input: n = 1 Output: 1 There is only one way to climb 1 stair
Input: n = 2 Output: 2 There are two ways: (1, 1) and (2)
Input: n = 3 Output: 3 (1, 1, 1), (2, 1), (1, 2)
Input: n = 4 Output: 5 (1, 1, 1, 1), (1, 1, 2), (2, 1, 1), (1, 2, 1), (2, 2)

Recursive Approach:
-
If the total_ways(N) is the total count of ways to reach Nth stair.
- If 1 step taken problem reduces to total_ways(N-1) .
- If 2 step taken problem reduces to total_ways(N-2) .
total_ways(N) = total_ways(N-1) + total_ways(N-2)
total_ways(N) = 1 step taken + 2 steps taken
-
Problem can be solved using fibonacci problem strategy.
Recursive Implementation:
def count_ways_to_nth_stair(N):
# If N <= 0 :- 0 or less stairs no ways to reach Nth stair
if(N <= 0):
return 0
# If N == 1 :- only 1 way walk 1 stair
# If N == 2 :- 2 ways ({1,1}, {2})
if (N == 1 or N == 2):
return N
# Else return no. of ways of reaching Nth stair by taking 1 step and 2 steps at once
return count_ways_to_nth_stair(N-1) + count_ways_to_nth_stair(N-2)
print("Example-1: count_ways_to_nth_stair(3)")
print(count_ways_to_nth_stair(3))
print("Example-2: count_ways_to_nth_stair(4)")
print(count_ways_to_nth_stair(4))
Output:

Dynamic Programming Approach:
If max 2 stairs can be climbed at once, then this problem can be solved by FIBONACCI problem strategy.
If max m stairs can be climbed at once, then this problem can be solved by MIN_COINS problem strategy.
7. Tiling Problem
Problem:
Given a “2 x n” board and “2 x 1” tiles, count the number of ways to tile the given board using the 2 x 1 tiles.
A tile can either be placed horizontally i.e., as a 1 x 2 tile or vertically i.e., as 2 x 1 tile.
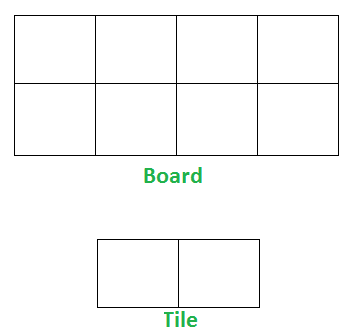
Example:
Input n = 3 Output: 3
Explanation:
We need 3 tiles to tile the board of size 2 x 3.
We can tile the board using following ways
1) Place all 3 tiles vertically.
2) Place first tile vertically and remaining 2 tiles horizontally.
3) Place first 2 tiles horizontally and remaining tiles vertically
Input n = 4 Output: 5
Explanation:
For a 2 x 4 board, there are 5 ways
1) All 4 vertical
2) All 4 horizontal
3) First 2 vertical, remaining 2 horizontal
4) First 2 horizontal, remaining 2 vertical
5) Corner 2 vertical, middle 2 horizontal
Recursive Approach:
-
Let total_ways(N) be the count of ways to place tiles on a “2 x n” grid, we have following two ways to place first tile.
- If we place first tile vertically, the problem reduces to total_ways(N-1).
- If we place first tile horizontally, we have to place second tile also horizontally and the problem reduces to total_ways(N-2).
total_ways(N) = total_ways(N-1) + total_ways(N-2)
total_ways(N) = 1 step taken + 2 steps taken
This problem like the previous can again be solved using fibonacci problem strategy.
Recursive Implementation:
def count_tiling_ways(N):
# If N <= 0 No way to put any tile
if(N <= 0):
return 0
# If N == 1 :- only 1 way put horizontal
# If N == 2 :- 2 ways either both horizontal or both vertical
if (N == 1 or N == 2):
return N
# Else return no. of ways of filling board by first putting 1 tile vertically or 2 tile horizontally
return count_tiling_ways(N-1) + count_tiling_ways(N-2)
print("Example-1: count_tiling_ways(3)")
print(count_tiling_ways(3))
print("Example-2: count_tiling_ways(4)")
print(count_tiling_ways(4))
Output:

8. Possible Decodings of Digit Sequence***
Problem:
Let 1 represent ‘A’, 2 represents ‘B’, . . . 26 represents ‘Z’ etc.
Given a digit sequence, count the number of possible decodings of the given digit sequence.
Examples:
Input: 121 Output: 3 coz Possible Decodings are: “ABA”, “AU”, “LA”
Input: 1234 Output: 3 coz Possible Decodings are: “ABCD”, “LCD”, “AWD”
Recursive Approach
- This problem is recursive and can be broken in sub-problems.
- Start from end of the given digit sequence.
- Initialize the total count of decodings as 0.
- Recur for two subproblems.
- If the last digit is non-zero, recur for remaining (n-1) digits and add the result to total count.
- If the last two digits form a valid character (or smaller than 27), recur for remaining (n-2) digits and add the result to total count.
Implementation:
def count_digits_sequence_decodings(digits):
n = len(digits)
# base cases
if(n==0 or n==1):
return 1
count = 0
# If the last digit is not 0, then last digit must add to the number of words.
if(digits[-1]>'0'):
count = count_digits_sequence_decodings(digits[:-1])
# If the last two digits form a number smaller than or equal to 26, then consider last two digits and recur
if(digits[-2]=='1' or (digits[-2]=='2' and digits[-1]<='6')):
count += count_digits_sequence_decodings(digits[:-2])
return count
print("Recursive Approach")
print("Example-1: count_digits_sequence_decodings('12')")
print(count_digits_sequence_decodings('12'))
print("Example-1: count_digits_sequence_decodings('121')")
print(count_digits_sequence_decodings('121'))
print("Example-3: count_digits_sequence_decodings('1234')")
print(count_digits_sequence_decodings('1234'))
Output:

Complexity:
- Time: Exponential
Dynamic Programming Approach
- If we take a closer look at the above program, we can observe that the recursive solution is similar to Fibonacci Numbers.
- Therefore, we can optimize the above solution to work in O(n) time using Dynamic Programming.
DP Implementation
def count_digits_sequence_decodings_DP(digits):
n = len(digits)
count = [0]*(n+1) # A table to store results of subproblems
# Base cases
count[0] = 1; count[1] = 1
for i in range(2, n+1):
count[i] = 0
# If the last digit is not 0, then last digit must add to the number of words
if (digits[i-1] > '0'):
count[i] = count[i-1]
# If the last two digits form a number smaller than or equal to 26,
# then last two digits form a valid character
if (digits[i-2]=='1' or (digits[i-2]=='2' and digits[i-1]<='6') ):
count[i] += count[i-2]
return count[n]
print("\nDP Approach")
print("Example-1: count_digits_sequence_decodings_DP('12')")
print(count_digits_sequence_decodings_DP('12'))
print("Example-1: count_digits_sequence_decodings_DP('121')")
print(count_digits_sequence_decodings_DP('121'))
print("Example-3: count_digits_sequence_decodings_DP('1234')")
print(count_digits_sequence_decodings_DP('1234'))
print("Example-3: count_digits_sequence_decodings_DP('1234121')")
print(count_digits_sequence_decodings_DP('1234121'))
Output:

Complexity:
- Time: O(n)
Next: Divide and Conquer Approach →